Componenti di un vettore in una base ortonormale. Matrici unitarie

martedì, Maggio 18th, 2021

vettore,componenti,base ortornormale,matrici unitarie

Sia {ei} una base ortonormale di uno spazio unitario n-dimensionale V. Quindi


essendo (α1,α2,...,αn) le componenti di ξ nella predetta base. Segue

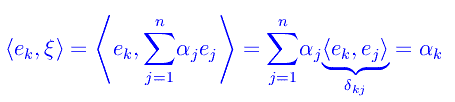
Quindi in una base ortonormale lo sviluppo di un qualunque vettore come combinazione lineare dei vettori di base, assume la forma:


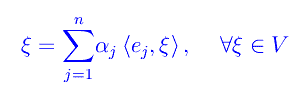
(altro…)



Posted in Algebra Lineare, Metodi matematici della fisica | No Comments »

[¯|¯] Legge di trasformazione delle componenti di un tensore covariante di rango 2

mercoledì, Febbraio 26th, 2020

tensore covariante di rango 2, componenti,legge di trasformazione

Scriviamo la matrice che ci fa passare dalla vecchia alla nuova base:


Siccome l'indice in alto è l'indice di riga, e quello in basso è l'indice di colonna, si ha:


Con ovvio significato dei simboli:


(altro…)



Posted in News | No Comments »