Curva regolare quale classe di equivalenza
mercoledì, Dicembre 16th, 2020
Approfondiamo le argomentazioni di una precedente lezione. Spesso si confonde una curva regolare con la sua rappresentazione parametrica. In realtà, una curva è una classe di equivalenza nell'insieme di tutte le rappresentazioni parametriche regolari (in uno spazio euclideo assegnato). In termini rozzi ma efficaci, una curva regolare è l'elemento che accomuna un insieme di rappresentazioni parametriche regolari. Il passaggio da una rappresentazione all'altra è realizzata da una riparametrizzazione che noi denominiamo sostituzione di parametro ammissibile. Si pensi ad esempio, alla traiettoria percorsa da una particella nello spazio fisico R^3. È chiaro che tale traiettoria può essere percorsa in infiniti modi possibili a seconda della velocità della particella. Le infiniti equazioni orarie sono rappresentazioni parametriche regolari. Al contrario, la traiettoria è unica ed è in un certo senso, il "sostegno" delle predette rappresentazioni parametriche.
Per maggiori dettagli, scarica la lezione in pdf
(altro…)




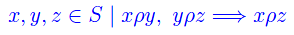




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











