[¯|¯] Relazioni di equivalenza. Classi di equivalenza
Giugno 29th, 2018 | by Marcello Colozzo |
Definizione
Una relazione ρ in un insieme S, si dice relazione di equivalenza se è riflessiva, simmetrica e transitiva.
Osservazione
Per quanto visto nel numero precedente, le proprietà di una relazione di equivalenza si traducono in proprietà del suo grafico. Precisamente, il grafico G(ρ) di una relazione di equivalenza è tale che
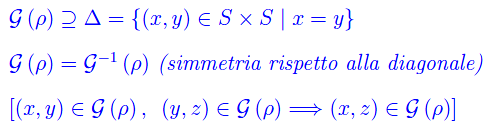
Proposizione 1
Comunque prendiamo una relazione di equivalenza ρ in S, si ha:

Dimostrazione
Proposizione 2
Comunque prendiamo una relazione di equivalenza ρ in S, si ha:

Dimostrazione
Implicazione diretta
Osserviamo innanzitutto che
Segue
Scomponiamo la doppia implicazione <=>
onde l'asserto.
Implicazione inversa
Per ipotesi
Per la proposizione precedente
Proposizione 3
Comunque prendiamo una relazione di equivalenza ρ in S, si ha:
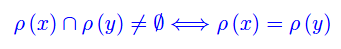
Dimostrazione
Implicazione inversa>
Per ipotesi
Per una proposizione dimostrata in una lezione precedente:
onde
da cui l'asserto.
Implicazione diretta
Ipotesi
Segue
Per quanto precede, se ρ è una relazione di equivalenza in S, comunque prendiamo x in S si ha che ρ(x) è non vuoto e contiene x come elemento.
Definizione
Il sottoinsieme ρ(x) di S, si dice classe di equivalenza rispetto a ρ.
Per la proposizione 2 comunque prendiamo y in ρ(x) si ha ρ(x)=ρ(y). Cioè, le due classi di equivalenza ρ(x) e ρ(y) coincidono per ogni y in ρ(x). In altri termini, ogni elemento di una assegnata classe di equivalenza determina la medesima classe. Ne consegue che una classe di equivalenza è univocamente determinata da un suo elemento preso ad arbitrio.
In virtù della proposizione 3, se y non appartiene a ρ(x) cioè se x e y individuano due classi ρ(x) e ρ(y) distinte, necessariamente queste ultime sono disgiunte.
D'altra parte, se se y non appartiene a ρ(x) significa che x e y non sono in relazione.
Conclusione
Elementi che non sono in relazione di equivalenza tra loro, determinano classi di equivalenza disgiunte.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

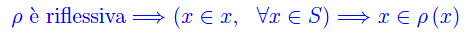
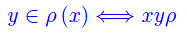
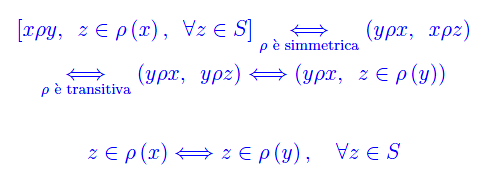
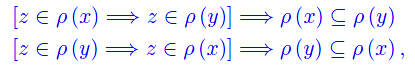
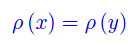
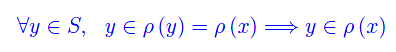
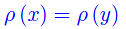
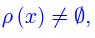
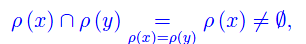




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











