[¯|¯] Ancora sul campo psi

lunedì, Dicembre 9th, 2019

meccanica quantistica,campo psi,funzione d'onda

In quest'articolo abbiamo introdotto un operatore hermitiano K che svolge un ruolo analogo all'operatore hamiltoniano H di un sistema quanto-meccanico nonrelativistico. Lo scopo è tentare una qualche descrizione dell'attività psichica di un organismo vivente. Incidentalmente, abbiamo denominato campo psi, il campo scalare matematicamente descritto da una funzione d'onda Ψ quale soluzione di un'equazione differenziale del tipo di Schrödinger:

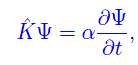
essendo α un numero immaginario puro, ovvero

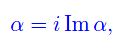
dove i è l'unità immaginaria, mentre Im(α) > 0 fissa le giuste dimensione per le varie grandezze. Se ci riferiamo a un sistema quanto-meccanico costituito da una sola particella nonrelativistica e priva di spin, si ha che l'operatore hamiltoniano non dipende esplicitamente dal tempo se il sistema è isolato. Precisamente:

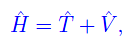
ove a secondo membro troviamo gli operatori corrispondenti alle osservabili energia cinetica ed energia potenziale:

(altro…)

Posted in Fantasticherie cognitive, Filosofia della Scienza | No Comments »

[¯|¯] Manifestazioni di un campo psi

sabato, Aprile 7th, 2018

campo psi,informazione,meccanica quantistica

Mi piace pensare allo "spazio della mente" come una sorta di spazio delocalizzato dove evolvono i pensieri. Qualcuno potrebbe chiedere: dove si trova questo spazio? Domanda lecita, ma errata poiché come ho scritto più sopra, lo spazio in questione è un "posto senza posto". Il nostro senso comune ora ci avverte che c'è qualcosa che non va. Ma è il senso comune ad essere limitato. Di spazi ne esistono infiniti e i matematici lo sanno benissimo. Cosa è più reale, lo spazio fisico (euclideo) in cui calpestiamo questo pianeta, o gli spazi di Hilbert dove oscillano le funzioni d'onda della meccanica quantistica?
(altro…)