[¯|¯] La funzione esponenziale integrale nel campo complesso

mercoledì, Aprile 19th, 2017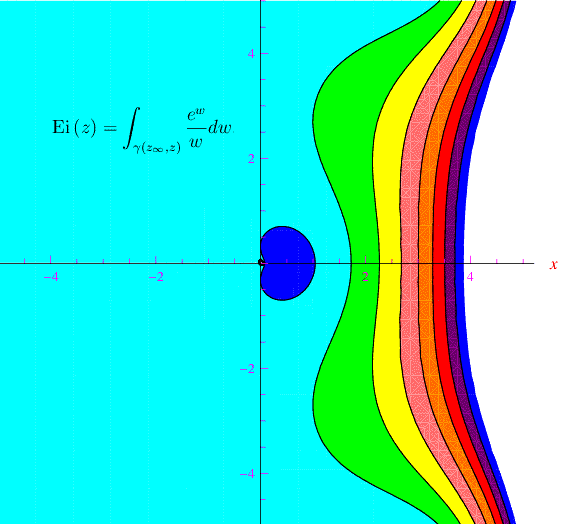

esponenziale integrale,campo complesso,integrale curvilineo,forma differenziale lineare — **Fig. 1**

Per estendere l'esponenziale integrale al campo complesso, è preferibile rammentare la nozione di integrale complesso. A tale scopo consideriamo una funzione f(z) della variabile complessa z=x+iy, che assumiamo continua in un campo connesso A del piano xy. Se z₀,z₁ appartengono al campo A, denotiamo con γ(z₀,z₁) un assegnato arco di curva generalmente regolare di estremi z₀ e z₁.
Definizione
Si dice integrale complesso della f(z) esteso a γ nel verso da z₀ a z₂, l'integrale curvilineo della forma differenziale lineare

esteso all'arco γ da da P₀(x₀,y₀) a P₁(x₁,y₁), essendo z₀=x₀+iy₀,z₁=x₁+iy₁. In simboli:

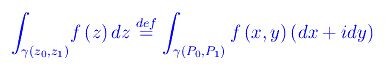
(altro…)

Posted in Analisi Matematica III | 1 Comment »

[¯|¯] La funzione esponenziale nel campo complesso

lunedì, Luglio 20th, 2015

Negli appunti di oggi trattiamo la funzione esponenziale nel campo complesso (in riferimento alla precedenti lezioni sulle funzioni olomorfe). Il nostro punto di partenza è la dimostrazione della formula: