La sinfonia aleatoria dei numeri primi
Maggio 30th, 2021 | by Marcello Colozzo |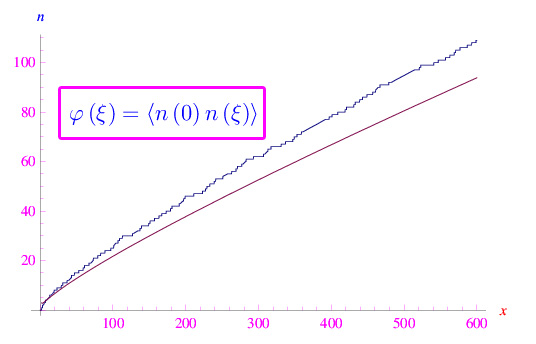
L'eventuale carattere aleatorio della legge di distribuzione dei primi è un'affascinante ipotesi di lavoro, che al contempo getta una luce ancora più sinistra sull'ipotesi di Riemann (in tal modo sarebbe altrettanto aleatorio il processo di distribuzione della parte immaginaria degli zeri non banali della funzione zeta di Riemann, "inchiodando" la parte reale a 1/2, i.e. assumendo per vera la predetta ipotesi).
A tale scopo denotiamo con n(x) il numero di numeri primi minori o uguali di x. Per tale funzione reale della variabile reale x, sussiste il teorema dei numeri primi

In fig. 1 il grafico di n(x) confrontato con quello di u(x). La ricerca della legge di distribuzione n(x) è un problema aperto. Tra l'altro, tale grandezza potrebbe essere una variabile aleatoria. In tal caso, il processo:

non è deterministico. Più precisamente, la conoscenza di n(x0) per un assegnato x0 > 2 determina univocamente la probabilità

Assumendo che il processo sia stazionario, si ha che tale probabilità non dipende da x, per cui la condizione di normalizzazione si scrive:

Ne seguono le tipiche grandezze statistiche (valor medio e varianza):

E quindi lo spettro di potenza della distribuzione dei primi:

la funzione di autocorrelazione:

Per il




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











