[¯|¯] Esempio di curva regolare dotata di rappresentazione parametrica non regolare
Febbraio 14th, 2020 | by Marcello Colozzo |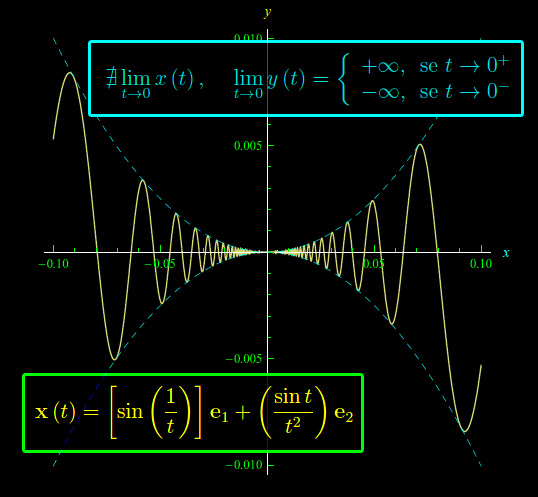
Da premettere che alcune nozioni come ad esempio, la riparametrizzazione nella sezione del blog dedicata alla geometria differenziale. Vale comunque la pena spendere qualche parola, tramite un esercizio molto istruttivo. Nello specifico è assegnata una rappresentazione parametrica che ha una singolarità per t=0 (t è il parametro).
Eseguendo un comune cambio di variabile parametrica, i.e. una riparametrizzazione, "sbattiamo" (scherzosamente parlando) la singolarità all'infinito, ottenendo in tal modo una rappresentazione parametrica regolare.
Vedremo tuttavia più avanti, che la rappresentazione parametrica non è regolare, poiché si annullano entrambe le derivate per θ=0.
Scarica l'esercizio in pdf
Tags: curva regolare, rappresentazione parametrica non regolare, riparametrizzazione
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











