[¯|¯] La lemniscata di Bernoulli

Dicembre 13th, 2016 | by Marcello Colozzo |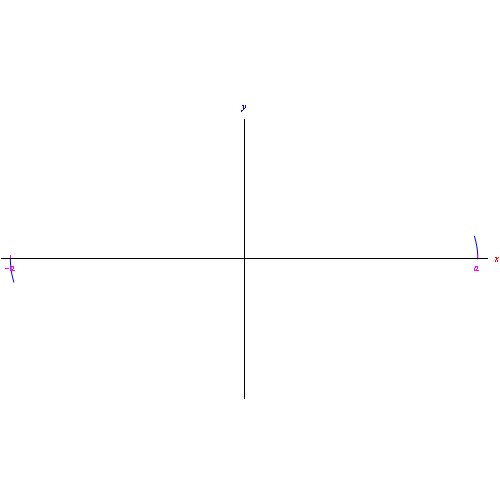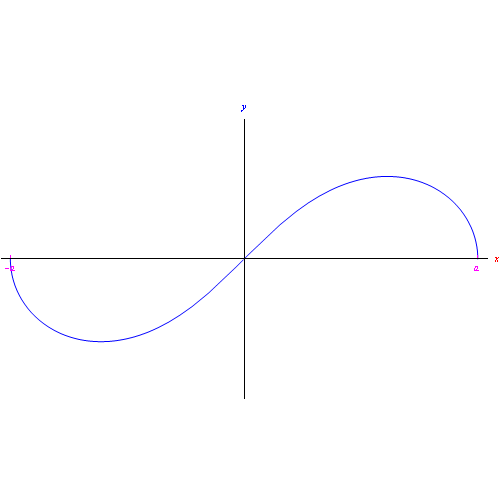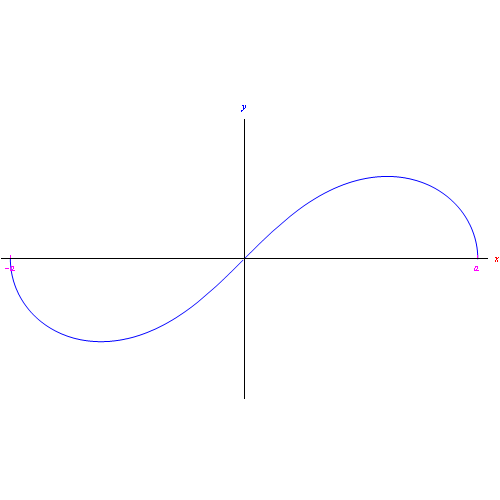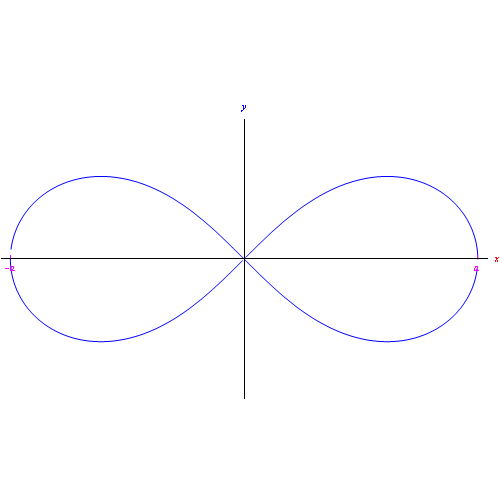

lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

Fig. 1

La lemniscata di Bernoulli ha equazione polare:

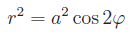
lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

Ne segue che se denotiamo con γ il luogo geometrico del piano la cui equazione in coordinate polari è data dalla equazione precedente, si ha:

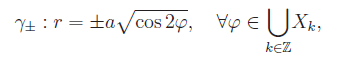
lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

ove

lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

essendo

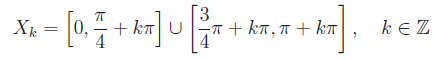
lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

Cioè la lemniscata è composta da due rami simmetrici rispetto all'asse polare.









Inserendo l'espressione
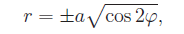
lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

nelle equazioni che esprimono le coordinate cartesiane in funzione delle coordinate polari, otteniamo la seguente rappresentazione parametrica dei predetti rami:
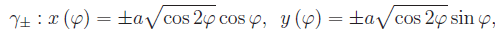
lemniscata di Bernoulli,coordinate polari,coordinate cartesiane

Scarica gli appunti in pdf

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , ,

Articoli correlati

Commenta l'esercizio