La funzione "arcotangente" dà luogo a punti di discontinuità di prima specie
Gennaio 21st, 2021 | by Marcello Colozzo |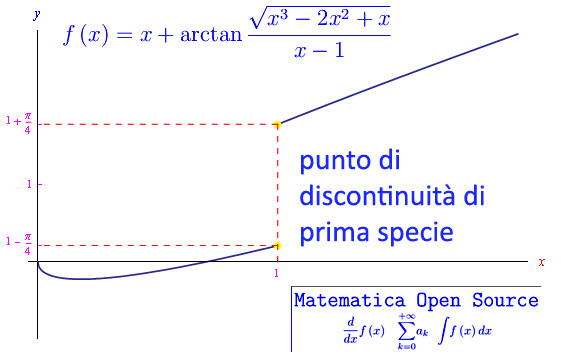
Esercizio
Classificare i punti di discontinuità della funzione riportata in fig. 1.
Soluzione
La funzione è definita su tutto il campo reale, escluso il punto x=1. Calcoliamo:

Occorre quindi risolvere la forma indeterminata 0/0

Per l'altro limite:

Quindi

Ne segue

Ne concludiamo che x=1 è un punto di discontinuità di prima specie.
Exercise
Classify the points of discontinuity of the function shown in fig. 1.
Solution
The function is defined on the whole real field, excluding the point x = 1. We calculate:

It is therefore necessary to solve the indeterminate form 0/0

For the other limit:

Therefore

It follows

We conclude that x = 1 is a discontinuity point of the first kind.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: arcotangente, arctan, Punti di discontinuità di prima specie
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











