» Esercizi svolti di Matematica e Fisica

Studio di un integrale generalizzato

Novembre 13th, 2020 | by Marcello Colozzo |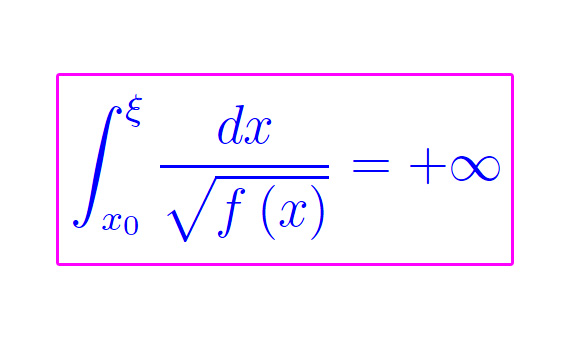

---

Sia f(x)=0 una funzione continua in [a,b], derivabile due volte in (a,b) con derivate continue. Se ξ è un punto interno di [a,b] ed è uno zero di f(x), necessariamente è un punto di minimo relativo, con f''(ξ) ≥ 0 (derivata seconda non negativa). Preso ad arbitrio un punto x₀ interno ad [a,b], ci proponiamo di studiare il comportamento del seguente integrale generalizzato

il cui estremo superiore di integrazione è un'evidente punto di discontinuità di seconda specie per la funzione integranda. Quest'ultima è comunque integrabile in [x0,xi;] giacché ha ivi segno costante. Per essere più specifici:

Per discutere la sommabilità applichiamo un noto criterio, che consiste nel determinare l'eventuale ordine di infinito dell'integrando nel predetto punto di discontinuità. Si tratta di studiare la seguente operazione di passaggio al limite:

Poniamo

Se α=1

Quindi:

• L'integrando è per ξ^-, un infinito del primo ordine:
  
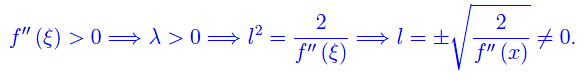
• L'integrando è per ξ^-, un infinito di ordine maggiore di 1:
  

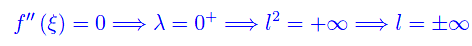
Segue che l'integrando è per ξ^-, un infinito di ordine maggiore o uguale di 1. Ne concludiamo che tale funzione non è sommabile in [x0,ξ].

Tags: funzioni integrabili, Funzioni sommabili, Integrali generalizzati

Articoli correlati