[¯|¯] Battendo (senza pizzicare) una corda infinitamente estesa
Ottobre 17th, 2018 | by Marcello Colozzo |
Abbiamo esaminato il caso 1. Passiamo ora alla corda (infinitamente estesa) e battuta, per cui inizialmente si trova nella configurazione di equilibrio, mentre il campo scalare della velocità iniziale è una assegnata funzione ψ(x). Quindi definiamo:

La soluzione del problema di Cauchy assegnato, si scrive:
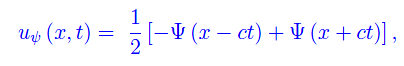
che è ancora una sovrapposizione di due onde piane che si propagano a velocità c in versi opposti. Nell'istante t=0 tali onde interferiscono distruttivamente, cancellandosi a vicenda:
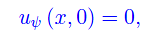
come appunto deve essere, giacché la corda è inizialmente in equilibrio. Ad esempio, se il campo di velocità iniziale è una gaussiana:
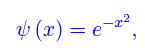
si ha

essendo erf(x) la funzione degli errori. In fig. 1 sono plottati gli andamenti delle varie grandezze, nonché la u(x,0) da cui vediamo che è identicamente nulla.

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
L'evoluzione dinamica della corda battuta con il campo di velocità assegnato, è
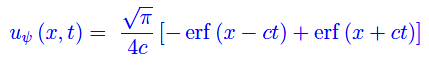
Per t=t1=8s presenta l'andamento riportato in figura:

Ciò non si verifica solo per una campo gaussiano come quello appena visto, ma è una proprietà generale a patto che la distribuzione sia sufficientemente piccata. Più precisamente, dato un campo di velocità iniziale ψ(x) sufficientemente piccato intorno a x=0 (o a un punto x0), si ha:
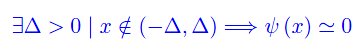
per cui
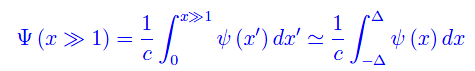
Cioè per x»1 la funzione ?(x) è approssimativamente costante. Ne consegue

onde lo spostamento a regime

che è una costante. In altri termini, la corda tende a traslare nell'istante in cui le onde componenti sono sufficientemente lontane.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: equazione della corda vibrante, equazioni differenziali alle derivate parziali, soluzione di D'Alembert
Articoli correlati

 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











