[¯|¯] Pizzicando una corda infinitamente estesa
Ottobre 16th, 2018 | by Marcello Colozzo |
Riscriviamo la soluzione di D'Alembert
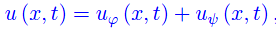
dove
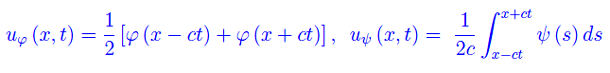
Cioè uφ(x,t) è la soluzione di D'Alembert se la velocità iniziale è nulla:

In tal caso si dice che la corda è inizialmente pizzicata. La funzione uψ(x,t) è, invece, la soluzione di D'Alembert se la configurazione iniziale è quella di equilibrio:

Abbiamo quindi i due casi particolari:
- corda inizialmente pizzicata;
- corda inizialmente battuta
Per quanto precede, nel caso 1 la soluzione di D'Alembert è una sovrapposizione lineare di due onde piane che si propagano lungo l'asse x con velocità c, è in versi opposti. In altri termini, il profilo iniziale φ(x) si scinde in due profili φ(x-ct) e φ(x+ct). Ad esempio, se il profilo iniziale è una gaussiana (in unità adimensionali):
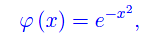
si ha a tutti i tempi:

come illustrato in fig. 1.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: equazione della corda vibrante, equazioni differenziali alle derivate parziali, soluzione di D'Alembert
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











