» Esercizi svolti di Matematica e Fisica

[¯|¯] Limiti di funzioni: quando la regola di De L'Hospital non è applicabile

Maggio 30th, 2018 | by Marcello Colozzo |

Sul gruppo facebook di matematica relativo a questo blog, un utente ha proposto il calcolo del seguente limite:

manifestamente equivalente a

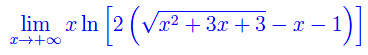
Dopo aver mostrato che l'argomento del logaritmo converge a 1, si ha che tale limite si presenta nella forma indeterminata 0·oo. Riconducendo tale forma alla 0/0 e applicando la regola di De L'Hospital, il limite non viene calcolato in quanto si ripresenta la 0·oo. Un altro utente ha risolto applicando l'analisi matematica non standard. Dal momento che non conosco tale paradigma di calcolo, cercherò di applicare una qualche manipolazione in modo da rimuovere l'indeterminazione.

In realtà tale limite appartiene a una classe di limiti derivanti da

dove:

1. f₁(x) diverge positivamente per x->x₀:
   
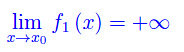
2. f₂(x) converge a 1 per x->x₀:
   

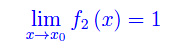
Abbiamo quindi la forma indeterminata:

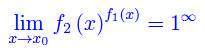
che viene ricondotta alla 0·oo scrivendo:

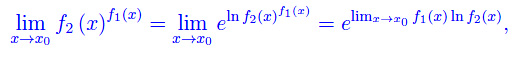
dove

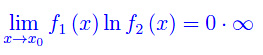
L'approccio usuale consiste nel convertire tale forma indeterminata nell'altra forma 0/0 per poi applicare la regola di De L'Hospital. Precisamente:

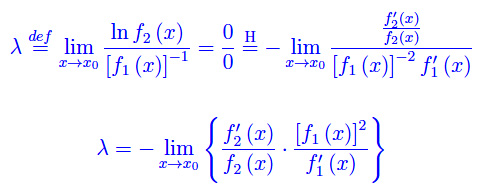
Riscriviamo

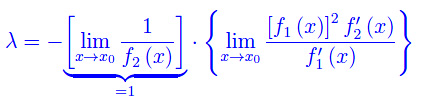
Tale procedimento non è rigoroso, poiché il teorema secondo cui il limite del prodotto di due funzioni è il prodotto dei limiti, può essere applicato se il prodotto è regolare in x0, cioè se è ivi dotato di limite. Tuttavia, proviamo ugualmente:

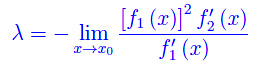
Se

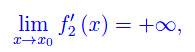
il limite λ si presenta nella forma indeterminata oo/oo che può essere forzata con la regola di De L'Hospital. Ma il caso interessante è x₀=+oo:

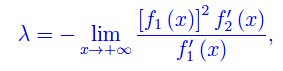
Evidentemente

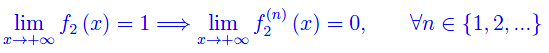
Ne consegue che si presenta nuovamente la forma indeterminata 0·oo, giacché

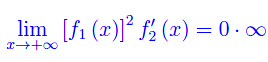
Forziamo con De L'Hospital:

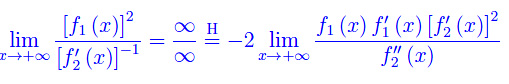
Ma

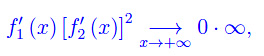
e così via se applichiamo nuovamente la predetta regola. Ne consegue che per il limite proposto, la regola di De L'Hospital fallisce. Bisogna, quindi, seguire altre strade che dipendono ovviamente dalle funzioni. Ad esempio:

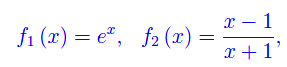
per cui

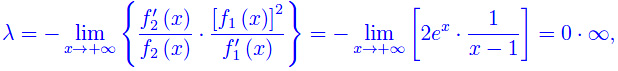
che si risolve banalmente per confronto tra infiniti:

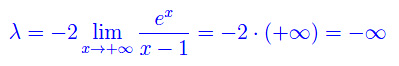
Consideriamo ora il caso proposto in precedenza:

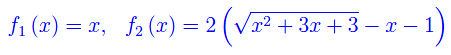
Eseguiamo il cambio di variabile x=(1/t)

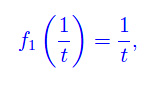
e

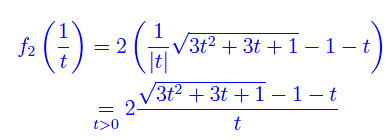
Quindi

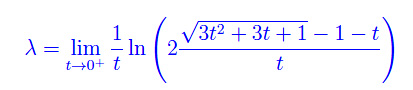
Poniamo

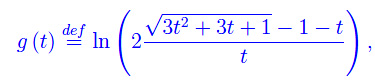
osservando che l'argomento del logaritmo ha una discontinuità eliminabile in t=0, giacché:

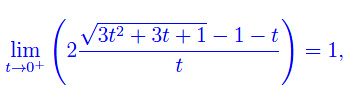
possiamo prolungare per continuità la funzione g(t), ponendo g(0)=0. A questo punto possiamo sviluppare g(t) in serie di Mac Laurin troncata a un ordine opportuno:

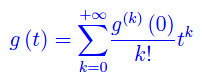
Calcolando le derivate:

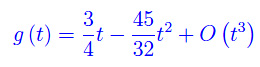
Segue, trascurando gli infinitesimi di ordine superiore al primo:

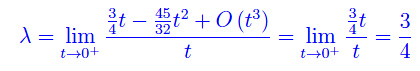
Sostienici

Tags: funzione, limite, regola di de l'hospital, sviluppo in serie

Articoli correlati