Annunci AdSense
Fig. 1. Alcune curve integrali dell'equazione differenziale assegnata.
Soluzione
Scrivendo l'equazione in forma normale
essendo
onde l'equazione è a variabili separabili. Ricerchiamone gli integrali costanti:
Ne consegue che l'equazione assegnata è priva di integrali costanti. Separando le variabili:
Integrando
Cioè
Sostienici
[¯|¯] Separando le variabili
Luglio 20th, 2017 | by Marcello Colozzo |Integrare l'equazione differenziale:
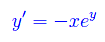
Soluzione
Scrivendo l'equazione in forma normale
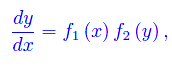
essendo
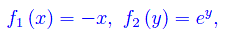
onde l'equazione è a variabili separabili. Ricerchiamone gli integrali costanti:
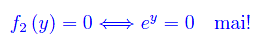
Ne consegue che l'equazione assegnata è priva di integrali costanti. Separando le variabili:
Integrando
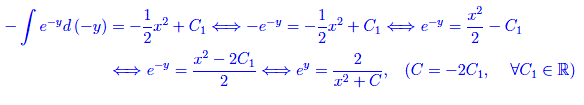
Cioè
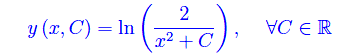
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Tags: Equazioni differenziali, integrale generale, separazione di variabili
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
