[¯|¯] Oscillazioni libere con attrito. Implementazione in Mathematica

Marzo 21st, 2017 | by Marcello Colozzo |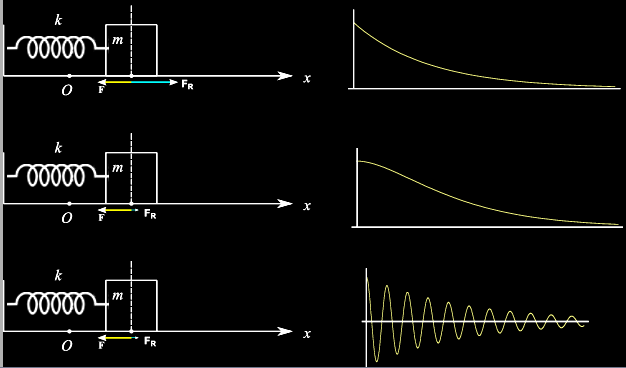

oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito — Fig. 1. Nell'oscillatore in alto, le forze di attrito sono dominanti, per cui nila particella non compie oscillazioni. Al centro una situazione simile, ma critica. L'oscillatore in basso compie oscillazioni esponenzialmente smorzate.

Ora che abbiamo compreso appieno la fisica del problema delle oscillazioni smorzate, ed aver risolto analiticamente l'equazione differenziale del moto per assegnate condizioni iniziali, possiamo affidarci a un software di calcolo simbolico/numerico come ad esempio, Mathematica. A tale scopo, riscriviamo l'equazione che ci interessa:

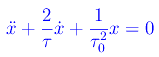
con le condizioni iniziali:
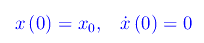
oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito

L'equazione differenziale è controllata dai parametri:

Dal momento che dobbiamo ricostruire in software l'evoluzione dinamica dell'oscillatore, è preferibile fissare una volta per tutte il valore di τ, lasciando come parametro la costante di tempo τ₀. Fisicamente, ciò equivale ad assegnare la forza di attrito e variare la costante elastica della molla. In tal caso è possibile ricostruire i tre casi:

I predetti comportamenti sono riassunti in fig. 1.

Ciò premesso, dopo aver settato nell'editor di Mathematica la costante di tempo dell'attrito:

oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
scriviamo l'equazione differenziale:

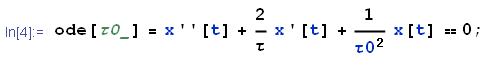
oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
Le condizioni iniziali:

oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
La soluzione è:

La seguente istruzione restituisce il grafico per un assegnato valore della costante di tempo:

oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
Ad esempio, qui abbiamo un comportamento aperiodico:

La velocità e l'orbita nello spazio delle configurazioni:

Ad esempio nel caso di aperiodicità:

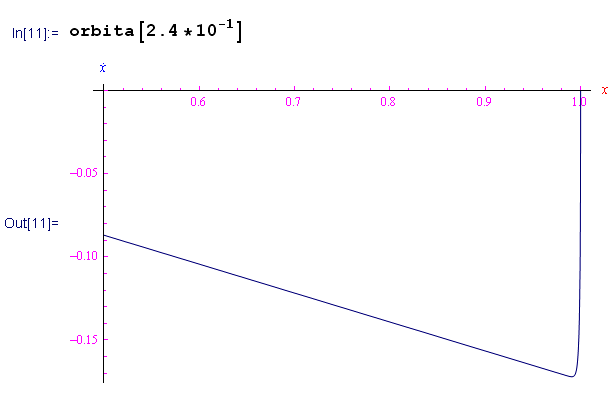
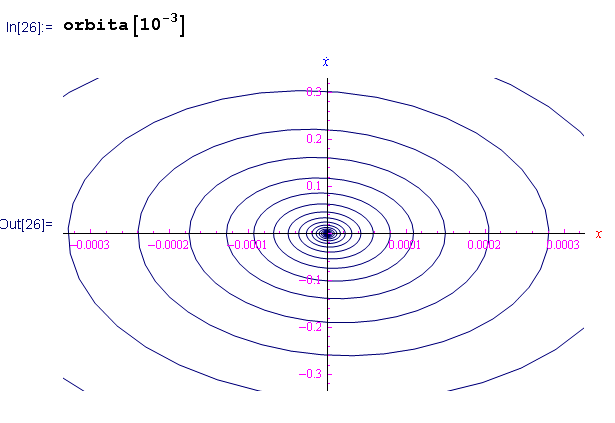
oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
Caso oscillatorio smorzato:

oscillatore armonico smorzato,decremento logaritmico,resistenza passiva,attrito
con orbita:

Per riprodurre il caso critico, non possiamo porre nelle istruzioni implementate τ=&tau₀, poiché nella soluzione si avrebbe uno zero a denominatore, per cui Mathematica restiuisce un messaggio di errore. Dobbiamo allora riscrivere l'equazione differenziale: