[¯|¯] Infinitesimi non dotati di ordine. Infinitesimi di ordine infinitamente grandi. Infinitesimi di ordine infinitamente piccolo
Febbraio 24th, 2017 | by Marcello Colozzo |
Fig. 1.
In questa Lezione abbiamo introdotto la nozione di infinitesimo [infinito] dotato di ordine. Osserviamo ora che non tutti gli infinitesimi [infiniti] sono dotati di ordine. Ad esempio nel caso degli infinitesimi, assegnata la classe I(x0) degli infinitesimi in x0 e non definitivamente nulli intorno a tale punto, e l'infinitesimo di riferimento:
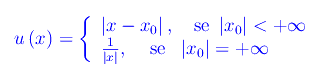
può accadere
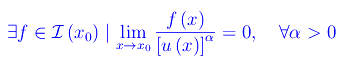
In tale circostanza diremo che f(x) è un infinitesimo di ordine infinitamente grande (rispetto a u(x)). Si badi che f(x) e u(x)α} sono comunque confrontabili. Pertanto, la confrontabilità è una condizione necessaria ma non sufficiente per l'esistenza dell'ordine di infinitesimo. Se invece:
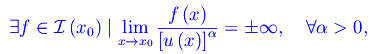
diremo che f(x) è un infinitesimo di ordine infinitamente piccolo (rispetto a u(x)).
Esempio 1
Assegnata la funzione
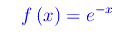
si ha
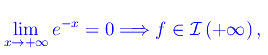
essendo I(+oo) la classe degli infinitesimi per x->+oo, non identicamente nulli intorno a x=+oo. Assumiamo come infinitesimo di riferimento la funzione:
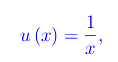
per cui calcoliamo
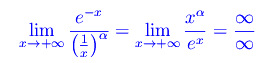
Applicando ripetutamente la regola di De L'Hospital:
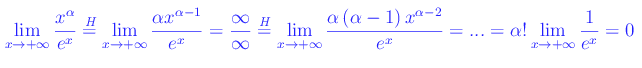
per cui e-x è (per x->+oo) un infinitesimo di ordine infinitamente grande.
Esempio 2
Assegnata la funzione
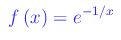
si ha
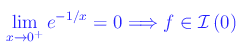
Assumendo come infinitesimo di riferimento
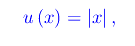
si ha
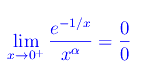
Eseguendo il cambio di variabile t=1/x e tenendo conto del risultato dell'esempio precedente.
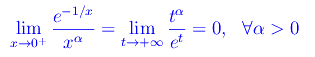
Ne concludiamo che la funzione assegnata è un infinitesimo (per x->0+) di ordine infinitamente grande. La funzione è graficata in fig. 1.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: infinitesimi di ordine infinitamente grandi, infinitesimi di ordine infinitamente piccolo, infinitesimi non dotati di ordine
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











