[¯|¯] Dipendenza lineare di un sistema di vettori
Dicembre 22nd, 2016 | by Marcello Colozzo |
Esercizio
Assegnato lo spazio vettoriale P3[t] dei polinomi di grado <=3 sul campo reale, si verifichi che il sistema
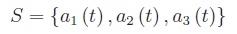
è linearmente indipendente, essendo:
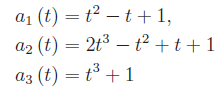
Soluzione
Scriviamo

Cioè
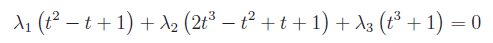
Sviluppando e ordinando i vari termini:
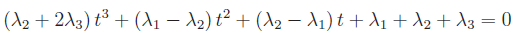
Il principio di identità dei polinomi restituisce il sistema lineare omogeneo nelle incognite λ1, λ2, λ3

la cui matrice dei coefficienti è
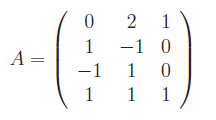
In generale il numero di soluzioni proprie (o autosoluzioni) di un sistema omogeneo è
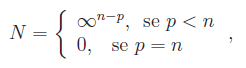
dove p=ρ(A) (rango di A), mentre n è il numero di incognite. Dobbiamo quindi calcolare il rango della matrice A. Il
minore
di ordine 3 ottenuto cancellando la quarta riga è:
Continua in pdf
No TweetBacks yet. (Be the first to Tweet this post)
Tags: polinomi, spazio vettoriale, vettori linearmente dipendenti
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











