[¯|¯] Passaggio da una rappresentazione parametrica qualsiasi alla rappresentazione naturale

Annunci AdSense

[¯|¯] Passaggio da una rappresentazione parametrica qualsiasi alla rappresentazione naturale

Dicembre 3rd, 2016 | by Marcello Colozzo |

rappresentazione parametrica,rappresentazione naturale,integrali ellittici

Esercizio
Scrivere la rappresentazione naturale del cammino di integrazione dell'esercizio precedente

Soluzione
Avevamo scritto

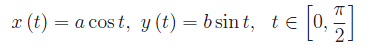
con l'ArcLenghtFactor dato da

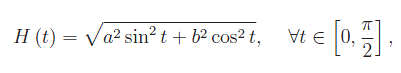
che non è identicamente uguale a 1.

Quindi la rappresentazione parametrica data non è la rappresentazione naturale. Fissiamo su γ(P,Q) un riferimento curvilineo con origine in P(a,0) e s contata positivamente in verso antiorario, cosicché
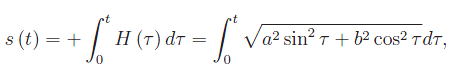
rappresentazione parametrica,rappresentazione naturale,integrali ellittici

che è un integrale ellittico di seconda specie. Ne consegue che non possiamo scrivere l'espressione analitica di s(t) e, quindi, determinarne l'inversa per poi passare alla rappresentazione naturale.

Scarica l'esercizio in pdf.s

No TweetBacks yet. (Be the first to Tweet this post)