Modelli predittivi del Covid nel paradigma dell'equazioni differenziali alle derivate parziali

martedì, Aprile 20th, 2021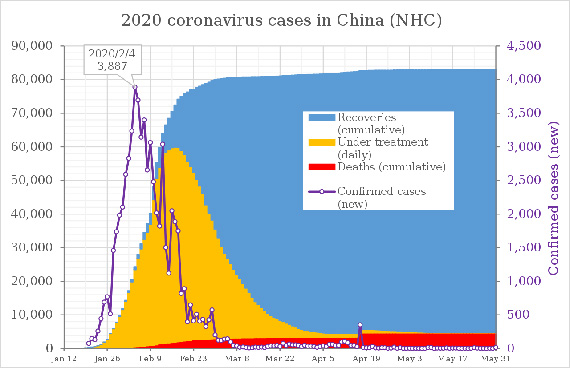

covid,modelli predittivi,equazioni differenziali alle derivate parziali

Introduzione. Onda pandemica

La maggior parte dei modelli predittivi di una qualunque pandemia sono basati su una schematizzazione di un virus del tipo macchina molecolare deterministica, matematicamente implementata da un sistema autonomo del tipo:

essendo f(y) lipschitziana onde esiste ed è unica la soluzione y(t) che enumera univocamente il numero di contagi nell'intervallo [t0,t]. Lo studio del ciclo vitale di una pandemia, è legato allo studio di funzione della derivata prima (rispetto al tempo) della predetta grandezza. Sotto ragionevoli ipotesi, ci si aspetta un comportamento del tipo di quello graficato in fig.:

che possiamo denominare onda pandemica. Assumendo la funzione y(t) analitica si ha che tale funzione e la sua derivata prima (è questa la grandezza interessante) non si annullano identicamente al finito. In particolare, per la derivata prima.

Tuttavia da un punto di vista operativo, è utile definire un «istante finale»

Ne segue che l'intervallo di tempo [t0,t1] è la durata della pandemia o ciclo vitale. Si osservi che l'esistenza di un istante finale è garantita da azioni di contenimento quali un lockdown λ e/o un vaccino ν.
Uno scenario più realistico prevede una successione di più onde pandemiche. In condizioni di idealità di propagazione virale (i.e. periodicità), si ha un andamento del tipo di quello riportato in fig.

Onda in propagazione. Sviluppo in armoniche sferiche

Per quanto precede, la grandezza interessante è la derivata prima della funzione y(t) che enumera gli «attuali positivi». La posizione:

esprime la dipendenza temporale di un processo di propagazione virale che è «funzione del posto», per cui siamo tentati a scrivere u(P,t). È ragionevole assumere un sistema di coordinate sferiche che si identifica con le usuali coordinate geografiche (latitudine e longitudine). Più precisamente, sulla sfera unitaria (rappresentativa della Terra) si ha u(θ,φ,t) essendo θ la colatitudine e &phi la longitudine. Denotiamo con u₀(θ,φ) il profilo iniziale dell'onda pandemica:

Precisamente

dove S2 è la sfera unitaria:

Si noti che ci riferiamo a grandezze complesse; fisicamente, significa che alla fine prenderemo la parte reale delle singole grandezze. Richiediamo la sommabilità del modulo quadro:

essendo dΩ=sinθdθdφ l'angolo solido elementare, mentre l'integrazione è estesa all'angolo solido totale (4π). Precisamente:

Come è noto, l'insieme L²(S₂) può essere strutturato come spazio vettoriale su C, introducendo le usuali operazioni di addizione di vettori e la moltiplicazione di uno scalare per un vettore, con relativi assiomi. Introducendo il prodotto scalare:

L²(S₂) assume una struttura di spazio di Hilbert, una cui base ortonormale è data dalle armoniche sferiche:

dove: N_lm è una costante di normalizzazione, e l=0,1,2,...,+oo, mentre per un assegnato l l'indice m assume i seguenti 2l+1 valori m=-l,-l+1,...,l-1,l; P_l^m(cosθ) sono le funzioni associate di Legendre:

essendo P_l(ξ) i polinomi di Legendre:

La costante di normalizzazione è data da:

Il sistema {Y^m_l(θ,φ)} è ortonormale e completo:

dove δ_ll' è il simbolo di Kronecker. La completezza garantisce che ogni elemento dello spazio funzionale L²(S₂) può essere espresso come combinazione lineare degli elementi della base {Y^m_l(θ,φ)}:

dove c°_lm sono le componenti del "vettore" u0(θ,φ) nella predetta base:

L'equazione scritta più sopra rappresenta lo sviluppo in armoniche sferiche di un'assegnata funzione u₀(θ,φ) di quadrato sommabile sulla sfera unitaria. Assumendo noto il profilo iniziale, si pone il problema dell'evoluzione temporale:

Congetturiamo che u(θ,φ,t) soddisfi una qualche «equazione d'onda» i.e. un'equazione differenziale alle derivate parziali del secondo ordine. Un'altra ipotesi ragionevole è la linearità e l'ordine 1 rispetto alla derivata temporale. Ne segue che a tutti i tempi, l'onda pandemica si esprime come:

dove i coefficienti c_lm(t) risolvono un'equazione differenziale ordinaria del primo ordine

tale da riprodurre il giusto andamento per u(t) come in fig.

Posted in Teoria dei sistemi dinamici | No Comments »

[¯|¯] Ottimizzazione termica di una cantina

venerdì, Gennaio 18th, 2019

equazione di conduzione del calore,equazioni differenziali alle derivate parziali,metodo di Fourier — .

La cantina ideale è fresca d'estate e calda d'inverno. Matematicamente, ciò si realizza a una profondità x tale da avere una "onda termica" in opposizione di fase (se in superficie la temperatura è alta, alla profondità x la temperatura è bassa, e viceversa). Si tratta, dunque, di risolvere l'equazione di conduzione del calore, che è una equazione differenziale alle derivate parziali. La ricerca delle soluzioni avviene tramite il metodo di Fourier.
(altro…)