Eserciziario di Algebra lineare
domenica, Gennaio 1st, 2023
Questo eserciziario è un veloce ripasso dei principali concetti di algebra lineare, utilissimi per affrontare questioni inerenti al formalismo matematico della meccanica quantistica (giusto per fare un esempio).
Argomenti:
- Operazioni sulle matrici
- Determinanti del second'ordine
- Determinanti del terzo ordine
- Determinanti del terzo ordine
- Determinanti di ordine qualsiasi
- Matrice aggiunta di una matrice quadrata
- Esempi di spazi vettoriali
- Applicazioni lineari. Omomorfismi ed endomorfismi
- Applicazioni singolari e non singolari. Isomorfismi
- Endomorfismi invertibili
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
(altro…)


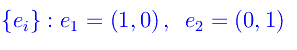
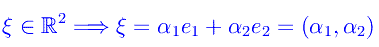


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











