[¯|¯] Densità degli zeri della funzione zeta di Riemann

Ottobre 8th, 2019 | by Marcello Colozzo |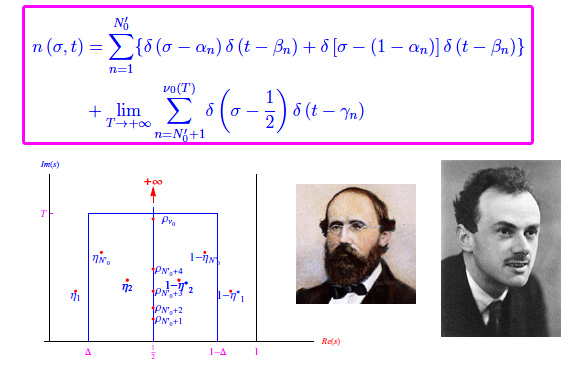

funzione zeta di Riemann,zeri,densità degli zeri, retta critica — **Fig. 1**

Riprendiamo lo sviluppo in serie della π₀(x)

rammentando che N'₀ < +oo è il numero di coppie di zeri (η_n,1-η_n^*) non appartenenti alla retta critica r_crit. La funzione H_N'₀(x) si esprime come

essendo

Qui ψ_n⁽¹⁾(x) e ψ_n⁽²⁾(x) sono a loro volta somme di serie di funzioni in cui compare la parte reale dell'esponenziale integrale paramentricamente dipendente dagli zeri η_n e ρ_n, ove questi ultimi sono tutti e soli quelli appartenenti alla retta critica. È chiaro che il pedice RH si riferisce all'ipotesi di Riemann, giacché il termine H_N'₀(x) si riduce a H_RH(x) assumendo la predetta ipotesi, giacché N'₀. Inoltre