» Esercizi svolti di Matematica e Fisica

[¯|¯] Inviluppo di una famiglia di curve piane

Dicembre 20th, 2018 | by Marcello Colozzo |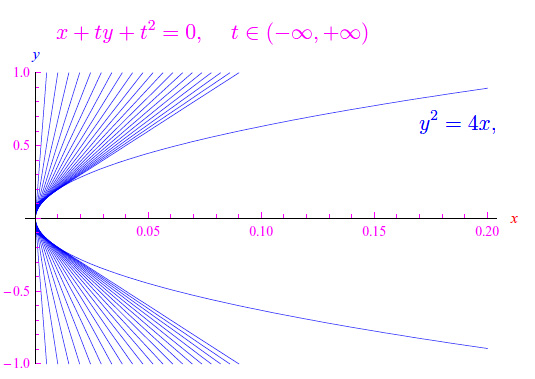

Consideriamo una famiglia (ad un parametro) di curve piane:

dove f è una assegnata funzione reale sufficientemente regolare. Per definizione di famiglia, un assegnato t in [a,b] individua univocamente una curva di Φ.

Definizione
Dicesi inviluppo per la famiglia Φ, una curva regolare Γ tale che per ogni suo punto P passi una ed una sola curva γ_t di Φ, la quale risulti in P tangente a Γ
Osservazione
La locuzione: γ_t è tangente a Γ nel punto P, equivale a quest'altra: γ_t e Γ hanno in P la medesima retta tangente.
Supponiamo che l'inviluppo sia dotato di una rappresentazione parametrica regolare

Per definizione di inviluppo, deve essere:

In generale è t' è diverso da t in quanto il primo parametro definisce una rappresentazione parametrica di Γ, mentre il secondo parametro seleziona una curva della famiglia Φ Possiamo comunque eseguire una sostituzione di parametro ammissibile (ovvero una riparametrizzazione di Γ) tale che t'=t:

Segue

L'equazione della retta tangente a Γ in P[x(t),y(t)] è

---

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

---

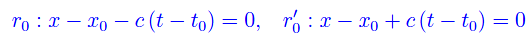
L'equazione della retta tangente a γ_t in P[x(t),y(t)] è

Tenendo conto dell'eq. precedente

D'altra parte, derivando primo e secondo membro della

si ha

Segue

Ne concludiamo che la curva inviluppo se esiste, ha una rappresentazione parametrica che è soluzione del sistema:

Alternativamente, si osserva che un punto (x,y) appartenente a γ_t e a Γ corrispondente a quell'assegnato valore di t che, in funzione di x,y, è univocamente determinato dalla

Da questa si ricava t=t(x,y). Ne consegue che (x,y) appartenente a Γ verifica l'equazione della γ_t(x,y)

Quest'ultima è l'equazione ordinaria (i.e. cartesiana) dell'inviluppo. La regola pratica consiste, quindi, nell'eliminare il parametro t tra le equazioni

Esempio
Determiniamo l'inviluppo della famiglia di rette:

Qui è

onde

Segue

Eliminando t

cioè una parabola, come illustrato in fig. 1.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: famiglia di curve piane, inviluppo, rappresentazione parametrica

Articoli correlati