» Esercizi svolti di Matematica e Fisica

[¯|¯] Il concetto di "Adesso" per il fisico Julian Barbour

Marzo 17th, 2018 | by Marcello Colozzo |

La fig. 1 mostra il moto di una freccia scoccata da un arco. Nel tentativo di negare l'esistenza oggettiva di un "tempo che scorre", Barbour asserisce nel suo libro che non esiste una sola freccia, ma tante (infinite) frecce quanti sono gli istanti di tempo compresi tra l'inizio e la fine del moto (quando la freccia colpisce il bersaglio, o comunque termina il suo moto). In altre parole, ogni istante è come se fosse congelato in ciò che Barbour denota "Adesso". È chiaro che gli "Adesso" sono intrinsecamente atemporali, e la diversità tra un Adesso e un altro (successivo o antecedente) determina l'ammontare del "tempo" tra i due "Adesso" considerati. Abbiamo, quindi, un intervallo temporale, ma si tratta di una illusione o meglio, di un artefatto della natura. Da questo punto di vista, il pensiero di Barbour collima con quello del famoso logico Kurt Gödel, secondo cui il Tempo è un "modo" tipicamente umano di percepire l'universo.

Anziché considerare una freccia, possiamo concentrare la nostra attenzione su qualcosa di molto più semplice e che può essere generato via software: il moto ideale di una pallina lungo una retta. La seguente animazione grafica.

La pallina si muove di moto uniformemente accelerato. È chiaro che per ragioni di spazio, il moto termina per poi ricominciare (loop). In realtà, la pallina dovrebbe muoversi indefinitamente lungo l'asse assegnato. Ma tutto questo non ha importanza per le nostre considerazioni. Infatti, qui non c'è alcuna pallina che si muove, ma semplicemente sono stati generati N "fotogrammi" ciascuno dei quali contiene una pallina rossa in una determinata posizione. La rapida successione dei fotogrammi genera l'illusione del movimento. Ricapitolando: non c'è alcuna pallina in movimento, ma N palline FERME.

Barbour nel suo libro definisce Platonia come lo spazio delle configurazioni relative dell'universo. È chiaro che l'universo è un sistema infinitamente più complesso di una semplice pallina. Per quest'ultima è assolutamente banale definire Platonia. Scriviamo innanzitutto l'equazione oraria del moto in unità adimensionali assumendo un'accelerazione unitaria:

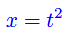
La velocità è la derivata prima della funzione x(t):

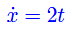
Eliminando il tempo t da tali equazioni

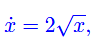
graficata in figura:

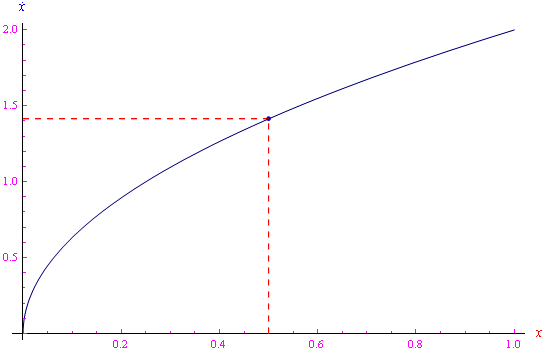
che definisce lo spazio delle configurazioni della particella. Precisamente, ogni punto della curva è un possibile "stato meccanico" della particella. Qui il tempo "è sparito", in quanto inglobato in un'unica equazione che definisce la velocità in funzione dell'ascissa della particella.

Per concludere, questo è solo un esempio banale di "Platonia", poichè nello spazio delle configurazioni che abbiamo appena definito, compare ancora l'ascissa x della particella, mentre Platonia deve "rimpiazzare" l'intero spaziotempo e quindi le coordinate spaziali.

Tags: julian barbour, la fine del tempo

Articoli correlati