» Esercizi svolti di Matematica e Fisica

[¯|¯] Equazioni differenziali che si integrano per separazione di variabili

Luglio 23rd, 2017 | by Marcello Colozzo |

Integrare l'equazione differenziale:

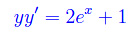
Soluzione
L'equazione è a variabili separabili. Per determinare gli eventuali integrali costanti, scriviamola in forma normale

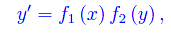
ove

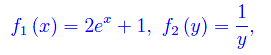
da cui vediamo che









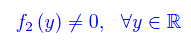
Ne segue che l'equazione data non ammette integrali costanti. Separiamo le variabili e integriamo

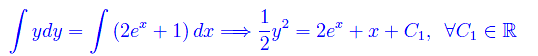
per ottenere l'integrale generale:

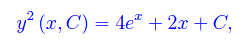
essendo C=2C₁.


Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: Equazioni differenziali, integrale generale, separazione di variabili

Articoli correlati