[¯|¯] Battimenti generalizzati a una qualunque coppia di funzioni periodiche
Marzo 16th, 2017 | by Marcello Colozzo |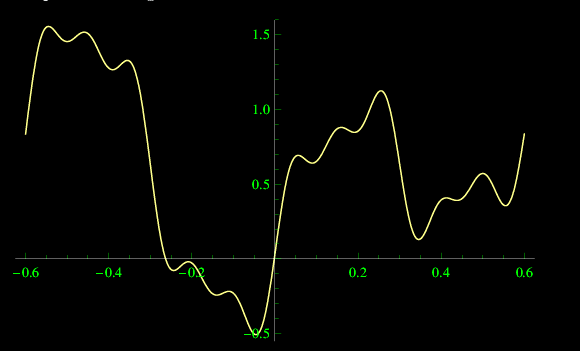
In questo post tenteremo di generalizzare il fenomeno dei battimenti a una coppia di funzioni periodiche non sinusoidali. A tale scopo riassumiamo i risultati raggiunti.
Abbiamo visto che comunque prendiamo due funzioni sinusoidali
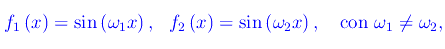
una qualunque combinazione lineare
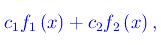
è un battimento se è verificata la condizione
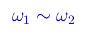
Senza perdita di generalità
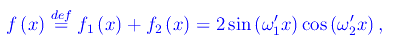
avendo applicato le formule di prostaferesi, per poi definire le nuove frequenze:
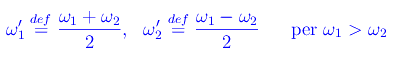
Segue
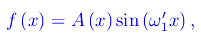
dove
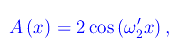
è un inviluppo di modulazione se è verificata la condizione

cioè se
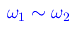
Supponiamo ora che f1(x) e f2(x) non siano funzioni sinusoidali, ma comunque periodiche e denotiamo con T1 e T2 i rispettivi periodi. Se tali funzioni verificano le condizioni di Dirichlet, possiamo scrivere i singoli sviluppi in serie di Fourier:
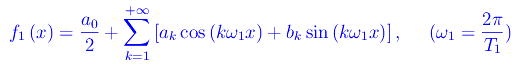
I coefficienti ak,bk sono dati da:
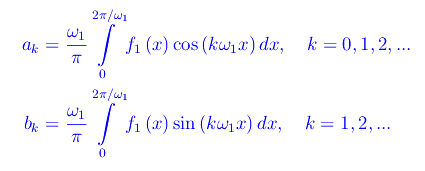
Per f2(x):
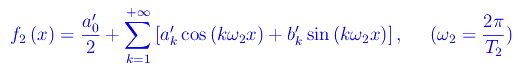
con formule simili per i coefficienti di Fourier a'k,b'k. Ricordiamo che la somma f1(x)+f2(x) è una funzione periodica se e solo se i periodi hanno in comune un multiplo minimo. Diversamente, non ha senso parlare di serie di Fourier associata alla funzione f1(x)+f2(x). In ogni caso proviamo a troncare entrambi gli sviluppi a un conveniente ordine di approssimazione N, per poi sommarli:
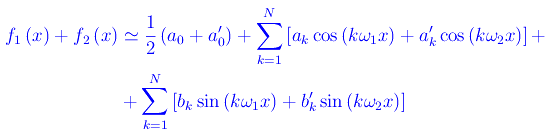
Vediamo quindi che i termini delle sommatorie danno luogo a battimenti se ω1~ω2. A titolo di esempio, consideriamo una funzione del tipo "dente di sega"
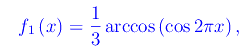
e un'altra del tipo "onda quadra":
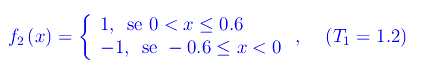
plottate in figura:
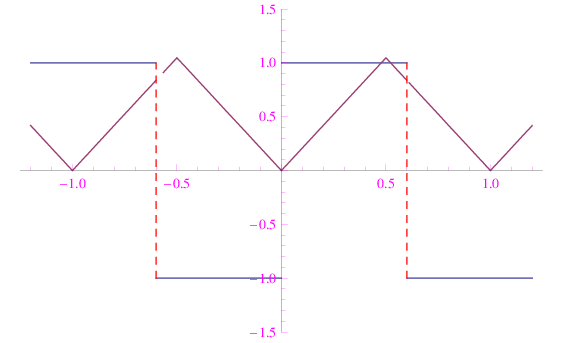
Si noti che tali funzioni sono periodiche con periodi leggermente diversi. La loro somma è plottata in fig.

Lo sviluppo in serie di Fourier della funzione a onda quadra, troncato al termine del quint'ordine è:

mentre lo sviluppo in serie di Fourier della funzione a denta di sega, troncato al termine del quint'ordine è:
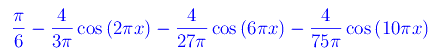
La loro somma è plottata in fig. 1 (al top di questa pagina).
Tags: battimenti, formule di prostaferesi, Funzioni periodiche
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











