Il Teorema di esistenza ed unicità e il Teorema del punto fisso
Marzo 4th, 2016 | by Marcello Colozzo |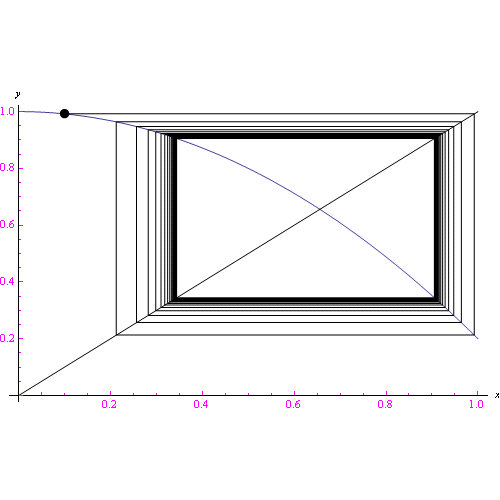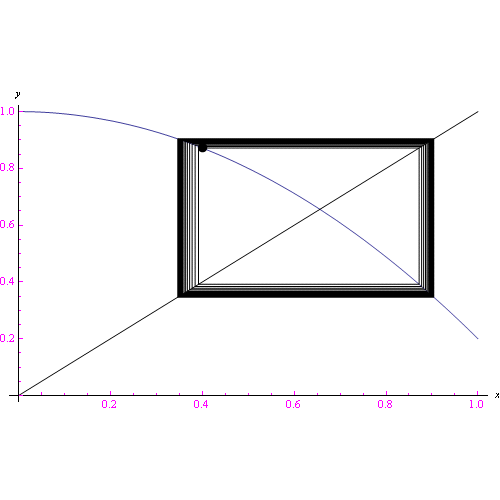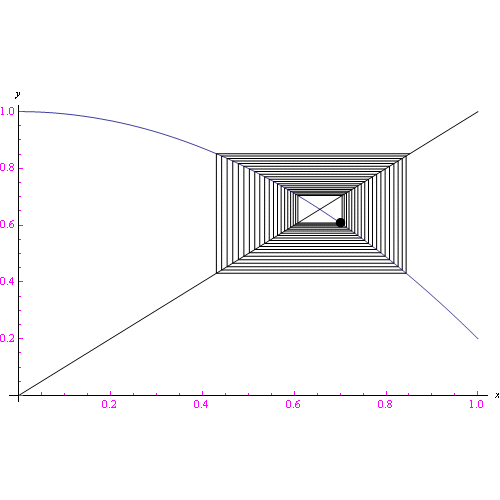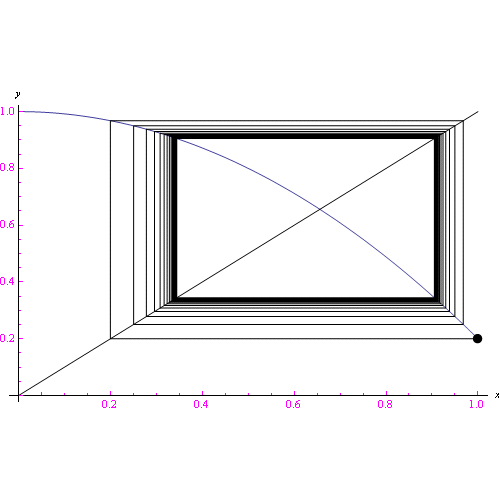
Riflettendo attentamente sui post precedenti, si potrebbe addirittura scoprire un legame tra il teorema di esistenza ed unicità delle soluzioni di un'equazione differenziale ordinaria del primo ordine di forma normale e autonoma, e il teorema del punto fisso. Per essere più specifici, consideriamo un sistema dinamico a tempo continuo la cui evoluzione è regolata da un'equazione differenziale del primo ordine x'=F(x), dove F non dipende esplicitamente dal tempo (il sistema è per ipotesi autonomo).
Come è noto, se F è lipichitziana il corrispondente problema di Cauchy ammette una sola soluzione. Eseguendo un campionamento discreto dell'intervallo temporale assegnato, si perviene a un sistema dinamico a tempo discreto con funzione di trasferimento f(x) il cui legame con F dipende dal sistema assegnato. Come abbiamo esaminato nei post precedenti, se la f(x) ha la derivata limitata nel proprio insieme di definizione da un numero reale minore di 1, l'algoritmo ricorsivo converge verso la radice dell'equazione f(x)=x (in sostanza è questo il teorema del punto fisso). Dinamicamente ciò vuol dire che il sistema evolve deterministicamente verso il punto fisso. Notiamo quindi una prima analogia "debole" con il teorema di esistenza ed unicità. Precisamente:
- Caso continuo. Affinchè il sistema sia deterministico, la funzione F(x) deve essere lipschitziana con coefficiente lambda.
- Caso deterministico Affinchè il sistema converga deterministicamente verso un punto fisso, deve essere |f'(x)| limitata da lambda minore di 1
Se facciamo cadere la condizione lambda minore di 1, l'evoluzione è ancora deterministica (e qui notiamo un analogia con il caso continuo, giacchè la corrispondente F(x) è lipschitziana), ma sarà accompagnata dalla comparsa di più attrattori> e per una particolare classe di funzioni, è caotica nel senso della teoria del caos. Una prima analisi è raccolta in questo file pdf
Tags: teorema del punto fisso, teorema di brouwer, teorema di esistenza ed unicità
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico












By STEFANO on Mag 8, 2017
Interessante, credo si possa usare per concludere elegantemente Fermat riscritto come:
C^n = 2\sum_{1}^{A} (X^n-(X-1)^n) + \Delta
C^n = 2\sum_{1}^{B} (X^n-(X-1)^n) - \Delta
dove:
\Delta = \sum_{A+1}^{B} (X^n-(X-1)^n)
Ho dimostrato che è possibile riscrivere queste sommatorie nei razionali in funzione di un divisore K (qualsiasi) e che portando K al limite si arriva all'integrale in cui nei termini (X^n-(X-1)^n)/K^n spariscono tutti tranne quello di grado maggiore che altro non è che quello che conosciamo come derivata Y'=nX^{n-1}.
Sul piano cartesiano:
In pratica Fermat definisce un'altezza (P) sulla curva Y=2X^n,
Il che implica un limite destro (irrazionale) per l'area sotto la sua derivata (e si chiede se P=C^n con C intero).
Usando questo teorema, se applicabile, diventa chiaro che l'unica soluzione possibile se la derivata non è lineare (unico caso in cui la radice n-sima di due, è la radica quadrata che moltiplicata per se stessa da 1),
è che \Delta sia infinitesimo, ovvero A=B.
Se non ti torna qualcosa alla pima lettura non cestinare, ci ho passato su 8 anni e la costruzione è corretta al 100%. La chiusura elegante, invece, è quella che bisognerà studiare e verificare insieme perchè è davvero il santo graal...
Ciao
Stefano
By Marcello Colozzo on Mag 8, 2017
Tranquillo, non cestino mai nulla. Anzi, grazie per il contributo!