» Esercizi svolti di Matematica e Fisica

Vettore tangente a una curva piana regolare

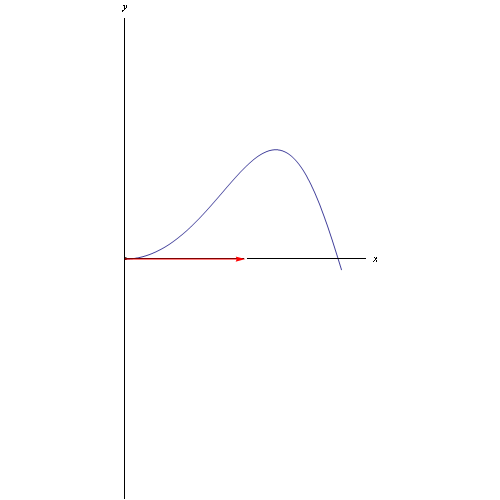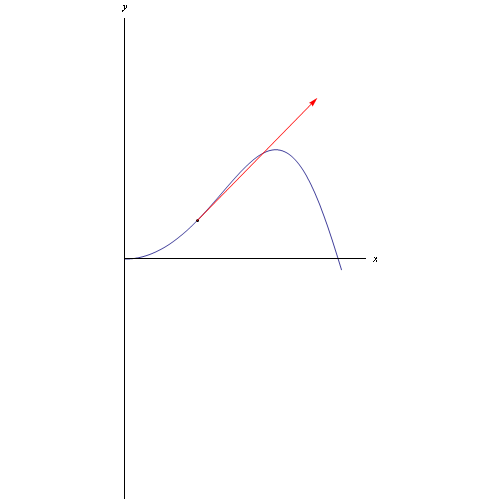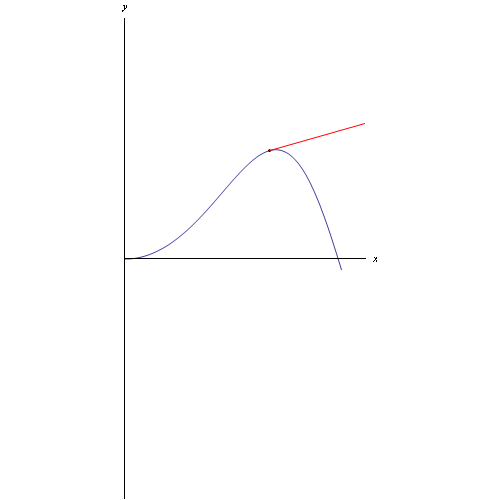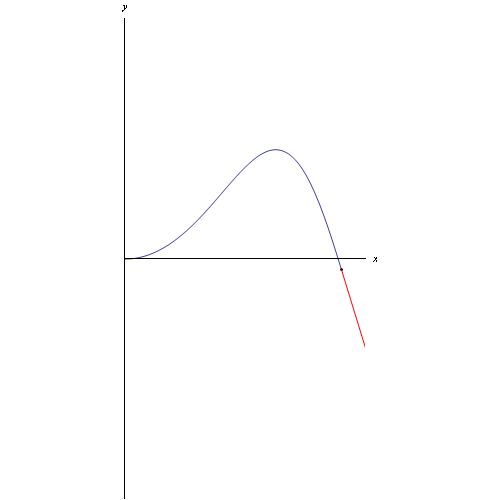
Nei post precedenti abbiamo affrontato l'interpretazione geometrica della derivata, trattando poi la questione dei punti angolosi. Ci rimangono da trattare i punti cuspidali o punti di regresso. Dal momento che questi ultimi si prestano ad una interessante intepretazione cinematica, vale la pena esaminare come tracciare il vettore tangente a una curva piana regolare, utilizzando il C.A.S. Mathematica.

Si tratta di "dare in pasto" a Mathematica una curva di rappresentazione parametrica x=x(t), y=y(t). Scriviamo:

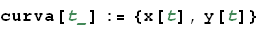
Riferiamoci, in particolare, alla seguente curva:

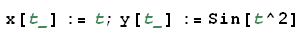
Per tracciare la curva e il relativo vettore tangente (che nel caso di un punto mobile rappresenta la velocità) utilizziamo il comando ParametricPlot con le appropriate opzioni:

Per i particolari analitici:
vettore_tangente_curva.pdf

Tags: curva piana, curva regolare, Mathematica, vettore tangente