» Esercizi svolti di Matematica e Fisica

[¯|¯] La funzione potenza di esponente reale

Novembre 27th, 2014 | by extrabyte |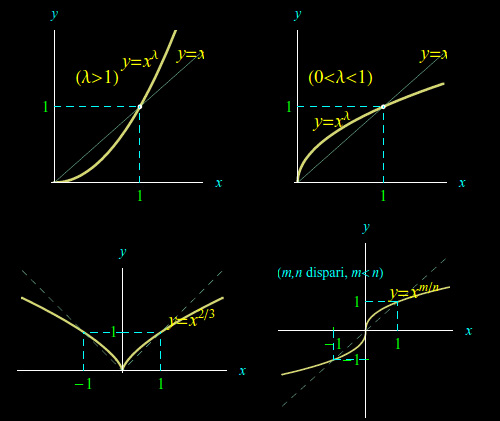

In questo post studiamo un'importante funzione elementare: la cosiddetta funzione potenza di esponente reale. Iniziamo il nostro studio considerando il caso speciale di esponente positivo. Tutto questo ci porterà fisiologicamente ad alcuni luoghi geometrici notevoli come la famosa parabola di Neile oltre alla generalizzazione del concetto di parabola (parabola di ordine m).

Definizione
Assegnato , dicesi funzione potenza di esponente reale, la funzione reale:. Cioè se:

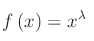
Per determinare l'insieme di definizione di tale funzione consideriamo:

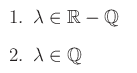
dove è l 'insieme dei numeri razionali. Prima di discutere i suddetti casi, assumiamo
. Nel caso 1, è irrazionale per cui la potenza ha significato solo per x non negativo. Quindi nel caso 1 l'insieme di definizione è X = [0,+oo).
Nel caso 2:

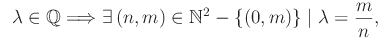
con m,n primi tra loro.

Pertanto:

Ciò implica:

Se

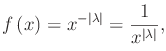
Tale relazione ci dice che per ciò che riguarda la ricerca dell'insieme di definizione.... Continua a leggere in PDF

Tags: funzione potenza di esponente reale, funzioni elementari, Insieme di definizione

Articoli correlati