[¯|¯] Premesse topologiche

sabato, Aprile 1st, 2017

spazio topologico,topologia,aperti,topologia banale — **Fig. 1. Copertina del saggio *La mente e l'infinito* del matematico Rudy Rucker.**

A un qualunque insieme S possiamo univocamente associare l'insieme i cui elementi sono tutti e soli i sottoinsiemi di S. Denotando con P(S) tale insieme, si ha:

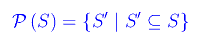
Definizione
Chiamiamo P(S) insieme delle parti di S.
L'insieme della parti di S è "strutturalmente" più complicato di S. Ad esempio, consideriamo l'insieme il cui unico elemento è la lettera a:
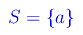
spazio topologico,topologia,aperti,topologia banale

I sottoinsiemi di S sono:
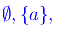
spazio topologico,topologia,aperti,topologia banale

onde

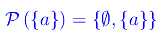
Aggiungiamo un elemento:
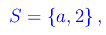
spazio topologico,topologia,aperti,topologia banale

i cui sottoinsiemi sono
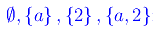
spazio topologico,topologia,aperti,topologia banale

Quindi

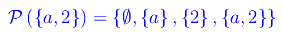
Se S è il vuoto? Cioè
spazio topologico,topologia,aperti,topologia banale

Segue

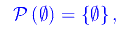
ovvero l'insieme delle parti del vuoto è l'insieme il cui unico elemento è il vuoto. Viceversa
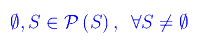
spazio topologico,topologia,aperti,topologia banale

Proposizione

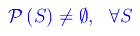
Dimostrazione
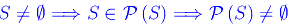
spazio topologico,topologia,aperti,topologia banale

c.d.d.
(altro…)

Posted in topologia | No Comments »

[¯|¯] Esercizi di Topologia

giovedì, Maggio 7th, 2015

Come complemento all'ebook Appunti di Topologia, pubblichiamo un file pdf con esempi di spazi topologici. Precisamente, verranno trattate la topologia banale e la topologia discreta, più lo spazio [0,1] non con la topologia standard (cioè euclidea). I passaggi sono svolti nei minimi dettagli.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Scarica l'ebook in formato PDF