[¯|¯] Tensori misti (applicazioni (r+s)-lineari)
venerdì, Marzo 6th, 2020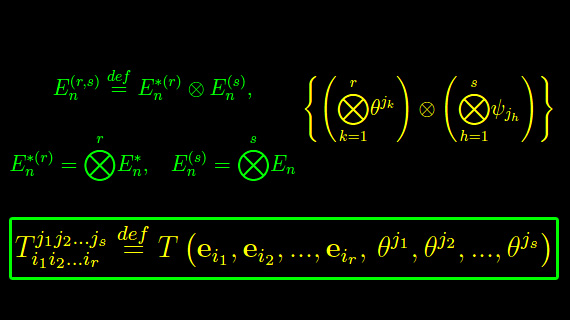
A questo punto la definizione di tensore misto è immediata. Precisamente, comunque prendiamo uno spazio vettoriale En su un campo K, possiamo definire un'applicazione (r+s)-lineare:
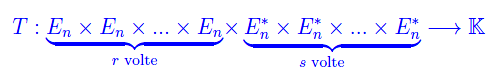
essendo (al solito) En* lo spazio duale di En. Quindi
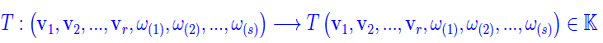
Definizione
La forma (r+s)-lineare (cfr. eq. scritta sopra), si dice tensore misto di rango r+s, di ordine di covarianza r e di ordine di controvarianza s (relativo allo spazio vettoriale En).
Se {ei} è una base di En e {θj} è la base duale ad essa associata, possiamo esprimere i singoli argomenti della predetta applicazione (r+s)-lineare, in termini di vettori di base:
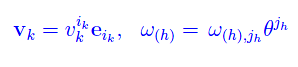
La (r+s)-linearità implica:
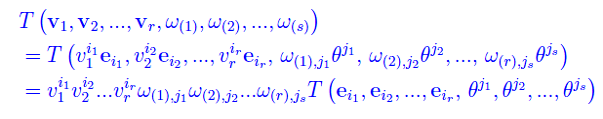
(altro…)

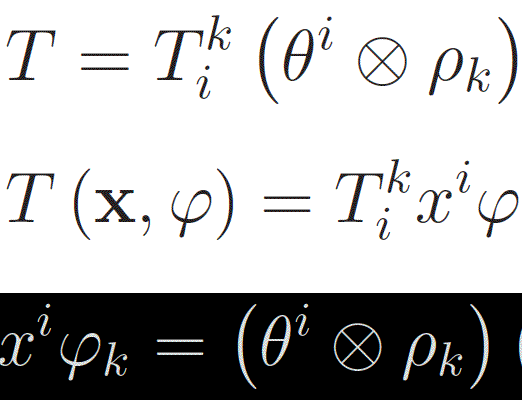


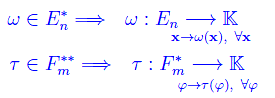



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











