[¯|¯] Tensori completamente simmetrici
mercoledì, Marzo 11th, 2020
Sia T un tensore covariante di rango r ovvero un'applicazione multilineare:

Definizione
Il tensore T si dice completamente simmetrico se la predetta applicazione è invariante rispetto a una qualunque permutazione dei suoi argomenti v1,v2,...,vr.
Tale definizione si generalizza immediatamente ai tensori controvarianti di rango qualsiasi. Inoltre, essa ha carattere intrinseco, ossia indipendente dalla base. Viceversa, il riferimento a una base restituisce la proposizione:
Proposizione
Un tensore r-covariante (o r-controvariante) è completamente simmetrico, se e solo se comunque prendiamo una base dello spazio vettoriale a cui esso appartiene, le sue componenti sono invarianti rispetto a una qualunque permutazione degli indici.
Dim.
Senza perdita di generalità, consideriamo un tensore doppio covariante:
Comunque prendiamo una base {ei} di En, è univocamente determinata la base duale {θj}
e quindi la seguente base di
cioè
cosicché
(altro…)


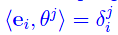

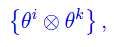
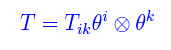
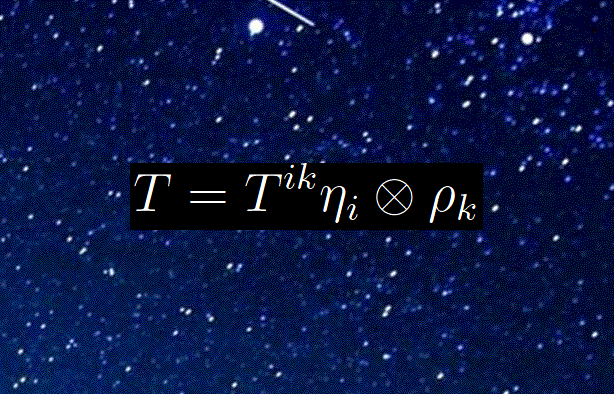
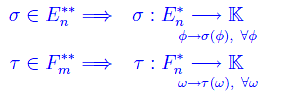
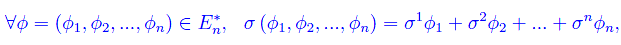
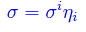


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











