Sottospazio vettoriale dei tensori completamente simmetrici

mercoledì, Marzo 18th, 2020

tensori completamente simmetrici,sottospazio vettoriale,matrici simmetriche — **Fig. 1**

Assegnato uno spazio vettoriale E_n e preso ad arbitrio un intero naturale r, consideriamo lo spazio prodotto tensoriale

e quindi, il suo sottoinsieme

i cui elementi sono i tensori r-covarianti completamente simmetrici. Mostriamo che si tratta di un sottospazio vettoriale di E_n^*(r). Infatti:

La chiusura di S_n^*(r) rispetto alle leggi di composizione di addizione di moltiplicazione per uno scalare, implica che tale insieme è un sottospazio vettoriale di E_n^*(r). Ovviamente siamo interessati alla dimensione di tale spazio. Intanto osserviamo che

(altro…)

Posted in Algebra Lineare | No Comments »

[¯|¯] Quando la somma non è una somma diretta

sabato, Luglio 1st, 2017

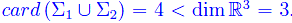
sottospazio ,sottospazio vettoriale,somma diretta,somma,intersezione

Esercizio
Nello spazio vettoriale R³ si considerino i seguenti sottospazi:

dove

Determinare una base della somma e dell'intersezione dei predetti sottospazi.

Soluzione
Il sistema di vettori Σ₁ è linearmente indipendente, per cui è una base di V₁ => dim(V₁)=2 Allo stesso modo dim(V₂)=2, giacché Σ₂ è linearmente indipendente. Riesce