Serie numeriche. Definizioni e prime proprietà

martedì, Ottobre 5th, 2021

serie numeriche,convergenza,somma,serie geometrica

Assegnata una successione di elementi di R:

la notazione

rappresenta formalmente la somma degli infiniti numeri u₀,u₁,...,u_n,.... Per assegnare un significato al simbolo

procediamo con un'operazione di passaggio al limite, definendo dapprima la somma parziale di ordine N:

quale elemento della successione di elementi di R:

È intuitivamente ovvio che il significato del simbolo con la sommatoria da 0 a +oo, è univocamente determinato dal comportamento all'infinito della successione delle somme parziali. Diremo, dunque, che il predetto simbolo è una serie numerica o semplicemente, una serie.
Definizione
La serie assegnata è convergente se tale è la successione delle somme parziali. Cioè se

Il numero reale S è la somma della serie e si scrive:

La serie assegnata è divergente se tale è la successione delle somme parziali. Cioè se

(altro…)

Posted in Analisi Matematica I | No Comments »

[¯|¯] Quando la somma non è una somma diretta

sabato, Luglio 1st, 2017

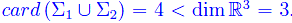
sottospazio ,sottospazio vettoriale,somma diretta,somma,intersezione

Esercizio
Nello spazio vettoriale R³ si considerino i seguenti sottospazi:

dove

Determinare una base della somma e dell'intersezione dei predetti sottospazi.

Soluzione
Il sistema di vettori Σ₁ è linearmente indipendente, per cui è una base di V₁ => dim(V₁)=2 Allo stesso modo dim(V₂)=2, giacché Σ₂ è linearmente indipendente. Riesce