Comportamento oscillante della somma di una serie di Dirichlet

lunedì, Ottobre 4th, 2021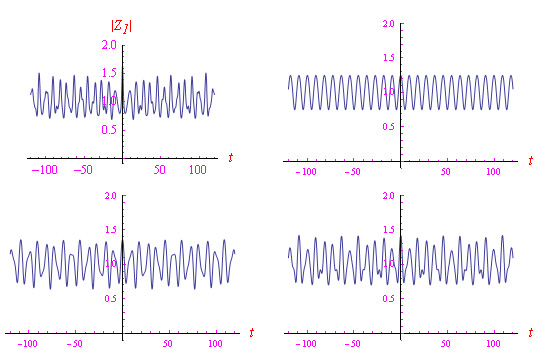

serie di Dirichlet,serie di fourier,funzione zeta di riemann — **Fig. 1**

Da un punto di vista formale esiste un'analogia tra una seriei di Dirichlet e una serie di Fourier. Come è noto, in quest'ultimo caso una qualunque funzione periodica f(t) (sufficientemente regolare), si esprime come sovrapposizione lineare di infinite componenti monocromatiche ciascuna di frequenza ω_n appartenenti a uno spettro che si distribuisce linearmente. Alla stessa maniera, la somma di una serie di Fourier valutata (in modulo) lungo una retta appartenente al dominio di convergenze) si esprime come sovrapposizione lineare di infinite componenti monocromatiche ciascuna di frequenza Ω_n=ln(n) appartenenti a uno spettro che si distribuisce logaritmicamente. Si badi che a differenza della f(t), la funzione data dalla somma della serie di Dirichlet non è periodica ma è comunque oscillante.
(altro…)

Posted in Analisi Matematica III | No Comments »

Serie di Fourier con Mathematica. Il caso dell'assegnazione condizionata

mercoledì, Aprile 15th, 2020

serie di fourier,fenomeno di gibbs, mathematica — **Fig. 1**

Mathematica dispone di vari package per l'analisi di Fourier. Tuttavia per funzioni definite con l'assegnazione condizionata, è necessario prestare attenzione. Infatti, un utilizzazione cieca di tali strumenti, conduce a risultati disastrosi. Conviene, allora, calcolare manualmente (e comunque via software) i coefficienti di Fourier.
(altro…)