[¯|¯] Riparametrizzazione. Sostituzione di parametro ammissibile. Curva regolare

mercoledì, Marzo 29th, 2017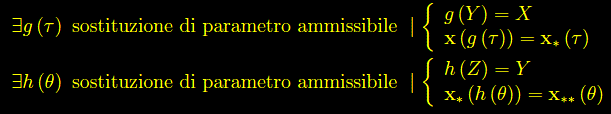

Sia data una rappresentazione parametrica di base X:

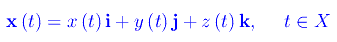
Eseguiamo il cambio di variabile t->τ, mediante la funzione t=g(τ) definita in un intervallo Y di R.
Definizione
La funzione g(τ) definisce una riparametrizzazione della rappresentazione parametrica assegnata.
Quindi scriviamo
alt=

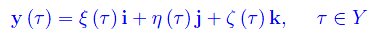
dove

Definizione
Una riparametrizzazione t=(τ) è una sostituzione di parametro ammissibile se:

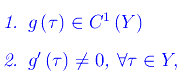
dove l'apice denota l'operazione di derivazione nella notazione di Lagrange:

Lemma
Una sostituzione di parametro ammissibile è invertibile.

Dimostrazione

Se g(τ) è una qualunque sostituzione di parametro ammissibile definita nell'intervallo Y, si ha: