Pendolo balistico

mercoledì, Marzo 3rd, 2021

Nel caso di un urto anelastico, il sistema costituito dai corpi collidenti non conserva l'energia cinetica. Per un urto normale centrale anelastico di due sfere (di massa m1 e m2) abbiamo una sola equazione che regola la dinamica unidimensionale dell'urto:

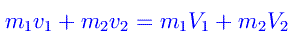
In particolare, se l'urto è perfettamente anelastico:

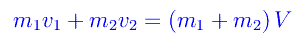
giacché dopo l'urto le due sfere traslano come un'unico sistema alla velocità V. Se una delle sfere è ferma:

Riesce

Fisicamente significa che se un corpo urta contro un ostacolo massivo (fermo), il corpo urtante ci si conficca arrestandosi. Nello specifico, consideriamo il pendolo balistico che permette di determinare la velocità di un proiettile. È un sistema costituito da un corpo massivo (di massa m2) estremamente deformabile (ad es., un sacco di sabbia) sospeso mediante una fune ideale di lunghezza l, ad un punto fisso C (fig. 1). Un proiettile (massa m2 < < m1) viene sparato a velocità v1 contro il sacco e si conficca in esso. Se il periodo T del pendolo è molto più grande della durata τ dell'urto, è lecito ritenere il pendolo in quiete durante τ. Ne segue che v2=0, per cui possiamo applicare l'equazione scritta più sopra che riscriviamo:

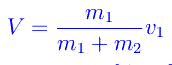
che è la velocità del sistema proiettile+sacco, subito dopo l'urto. In seguito a tale velocità il centro di massa del sistema raggiunge una quota H tale che l'energia cinetica è convertita in energia potenziale del campo di gravità:

da cui

Dalla fig. 1 H=l(1-cosθ)

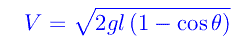
che confrontata con l'eq. scritta più sopra ci permette di ricavare la velocità del proiettile:

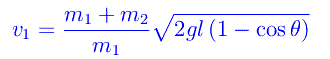
a patto di misurare l'angolo di deviazione θ. Ad esempio:

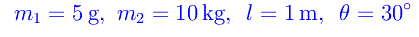
Quindi

L'energia cinetica iniziale del sistema è quella del proiettile in quanto il sacco è in quiete:

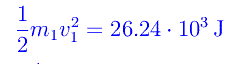
L'energia cinetica subito dopo l'urto è

da cui vediamo che quasi tutta l'energia cinetica è dissipata in calore.

(altro…)

Posted in Fisica generale 1 | No Comments »

Urto proiettile-pendolo balistico

martedì, Ottobre 14th, 2008

Un proiettile di massa m = 4 g va ad urtare, con una velocità di 600m/s, contro un pendolo balistico di massa M = 1 kg e di spessore 25 cm (inizialmente fermo). Il proiettile passa attraverso il pendolo ed emerge con una velocità di 100 m/s. Calcolare la forza frenante (costante nel tempo) che agisce sul proiettile durante il passaggio attraverso il pendolo e determinare l’altezza alla quale il pendolo stesso, sale.

(altro…)