Propagazione ondosa e dispersione

domenica, Maggio 2nd, 2021

onde di de broglie,onde elettromagnetiche,pacchetto d'onde

Onde di De Broglie
Qui l'equazione d'onda è l'equazione di Schrödinger per una particella libera:

dove per semplicità consideriamo una propagazione unidimensionale. Ricerchiamo soluzioni del tipo onda piana monocromatica, che con ovvio significato dei simboli si scrivono:

Ricordiamo che k e ω sono rispettivamente il numero d'onde e la frequenza (angolare). Imponendo che ψ sia soluzione si trova:

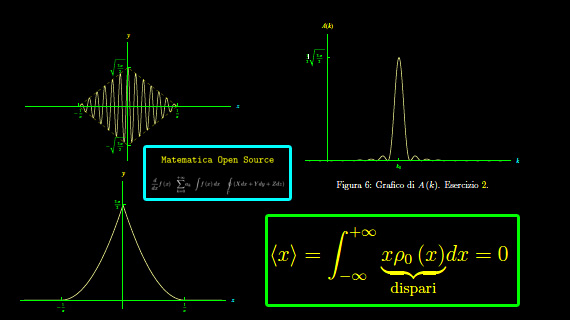
La funzione ω(k) ci dà delle informazioni sulla dispersione, nel senso che considerando una sovrapposizione lineare di onde monocromatiche (pacchetto d'onde), le singole componenti monocromatiche si propagano alla velocità di fase:

che differisce dalla velocità di gruppo (con cui avviene il trasporto di energia):

da cui vediamo che i conti tornano, nel senso che troviamo la velocità classica della particella descritta da un'onda di De Broglie piana e monocromatica.

(altro…)

Posted in Meccanica Quantistica | No Comments »

Incertezza sulla posizione di una particella la funzione d'onda è un pacchetto d'onde

mercoledì, Maggio 13th, 2020

pacchetto d'onde,posizione,particella,indeterminazione

Continuiamo l'esercizio di ieri.

Per calcolare la deviazione quadratica media Δx, dobbiamo dapprima calcolare i valori medi e sullo stato definito dalla funzione d'onda ψ₀(x), giacché

avendosi

essendo ρ₀(x)=|ψ₀(x)|² la densità di probabilità di trovare la particella in un assegnato intervallo infinitesimo [x,x+dx]. Abbiamo, dunque

che può essere prolungata per continuità in x=±1/a, avendosi ρ₀(±1/a)=0. La funzione ρ₀(x) è manifestamente pari e il suo grafico in [-1/a,1/a] è l'unione di due archi di parabola aventi vertici in (±1/a,0) rispettivamente. Ad occhio vediamo che =0. Più precisamente