Entropia di una pandemia

lunedì, Ottobre 18th, 2021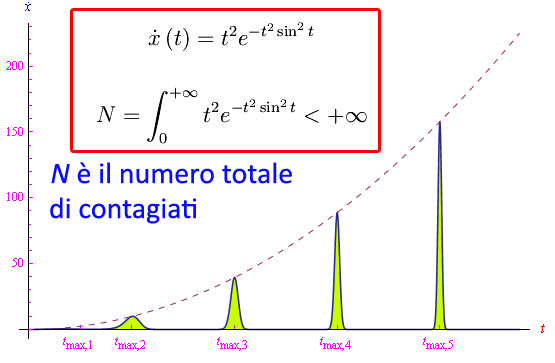

pandemia,entropia,funzioni sommabili — **Fig. 1**

Denotiamo con x(t) la funzione che enumera i contagiati da inizio pandemia. Ne consegue che la derivata prima di tale funzione:

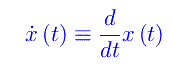
esprime il tasso giornaliero dei contagi (a rigore, dovremmo dapprima campionare la variabile tempo in giorni). Supponendo che tali funzioni siano definite in [0,+oo), il numero di contagiati totali è dato dal seguente integrale generalizzato:

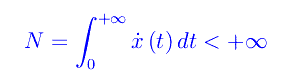
che è necessariamente convergente. Quindi, un qualunque modello matematico di pandemia è caratterizzato da una funzione

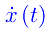
sommabile in [0,+oo). Un modello realistico è quello in cui tale funzione è, per t->oo, un infinitesimo di ordine maggiore di 1 (rispetto all'infinitesimo di riferimento 1/t). Più precisamente, possiamo modellizzare il processo pandemico attraverso un sistema dinamico autonomo con un'assegnata condizione iniziale che dà luogo al seguente problema di Cauchy:

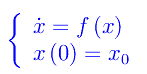
In tale classe di sistemi autonomi, selezioniamo tutti e soli quelli caratterizzati da una derivata prima della funzione x(t), sommabile in [0,+oo). Con ovvio significato dei simboli:

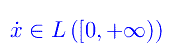
(altro…)

Posted in Teoria dei sistemi dinamici | No Comments »

Studio di un integrale generalizzato

venerdì, Novembre 13th, 2020

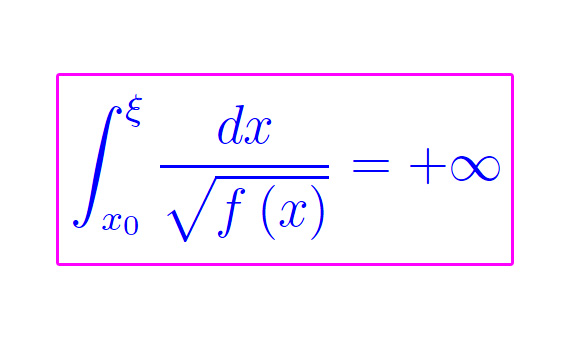
integrali generalizzati,funzioni integrabili,funzioni sommabili

Sia f(x)=0 una funzione continua in [a,b], derivabile due volte in (a,b) con derivate continue. Se ξ è un punto interno di [a,b] ed è uno zero di f(x), necessariamente è un punto di minimo relativo, con f''(ξ) ≥ 0 (derivata seconda non negativa). Preso ad arbitrio un punto x₀ interno ad [a,b], ci proponiamo di studiare il comportamento del seguente integrale generalizzato

il cui estremo superiore di integrazione è un'evidente punto di discontinuità di seconda specie per la funzione integranda. Quest'ultima è comunque integrabile in [x0,xi;] giacché ha ivi segno costante. Per essere più specifici:

Per discutere la sommabilità applichiamo un noto criterio, che consiste nel determinare l'eventuale ordine di infinito dell'integrando nel predetto punto di discontinuità. Si tratta di studiare la seguente operazione di passaggio al limite: