[¯|¯] Spazio vettoriale delle funzioni di una variabile reale

lunedì, Dicembre 19th, 2016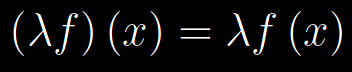

spazio vettoriale,assiomi,funzioni continue,addizione,scalari

Assegnato un intervallo [a,b] del campo reale R, è consuetudine denotare con C([a,b]) l'insieme delle funzioni reali continue in [a,b]. Introduciamo in C([a,b]) le ordinarie operazioni di addizione di funzioni e di moltiplicazione di uno scalare (elemento di R) per una funzione. Più precisamente, definiamo "somma di f(x) e g(x)" la funzione:

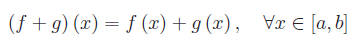
L'elemento neutro rispetto all'addizione è la funzione identicamente nulla, mentre l'elemento opposto di f(x) è -g(x). L'operazione di moltiplicazione di uno scalare per un elemento di C([a,b]) è così definita:

È facile persuadersi che l'insieme C([a,b]) assieme alle operazioni sopra definite (+,·), verifica tutti gli assiomi di spazio vettoriale. Ne concludiamo che (C([a,b]),+,-) è uno spazio vettoriale su R.
(altro…)

Posted in Algebra Lineare | No Comments »

Classificazione dei punti di discontinuità di una funzione

martedì, Marzo 29th, 2016

funzioni continue,punti di discontinuità, punti di singolarità

Questo esercizio chiede di classificare i punti di discontinuità di una funzione reale di una variabile reale. Come è noto, in questi casi occorre dapprima ricavare l'insieme di definizione, dopodichè si determina il comportamento della funzione in un intorno dei punti di accumulazione di tale insieme non appartenenti ad esso.
(altro…)