n blocchi legati da una fune inestensibile
giovedì, Giugno 18th, 2020
Generalizzare l'esercizio precedente al caso di n blocchi di massa m disposti come in fig. 1. Assumere come grandezze note la massa m e la tensione T12 sul blocco A1. Le quantità da calcolare - lasciandole inespresse - sono la forza trainante F supposta costante, e l'accelerazione con cui l'intero sistema trasla. Supponendo che il carico di rottura sia T0, determinare il massimo valore consentito per la forza trainante. Riguardo a quest'ultimo quesito, si discuta il limite per n->+oo.
Soluzione
Applicando il secondo principio della dinamica all'intero sistema, si ha:

Dal momento che conosciamo la tensione T12, il predetto principio applicato al blocco A1 restituisce:

per cui l'accelerazione è

mentre la forza trainante vale
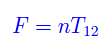
Constatiamo che la massa di singolo blocco sembra non giocare alcun ruolo per il valore di F. In realtà, la massa m è per così dire, inglobata nella tensione T12.
Analizzando le forze agenti sul blocco A2 attraverso il secondo e il terzo principio della dinamica, si ottiene con ovvio significato dei simboli

Alla stessa maniera, ragionando sul blocco successivo:

(altro…)



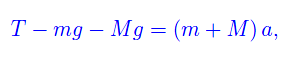
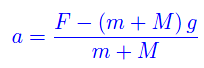


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











