La coscienza dei Robot potrebbe non percepire il trascorrere del Tempo

domenica, Agosto 22nd, 2021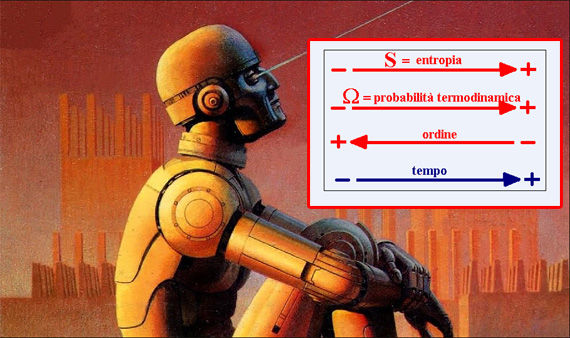

coscienza, robot, freccia del tempo termodinamica

Alcuni spunti di riflessione innescati da questo post

Metafora informatica

Vi siete mai chiesti perché la memoria di un computer è infallibile? Più specificatamente, se cerchiamo un determinato file memorizzato sull'hard disk, il sistema operativo e la relativa applicazione, ce lo restituisce così com'era, senza "dimenticanze" (umanamente parlando). Tale infallibità deriva dal fatto che la predetta memoria conosce una "bassa entropia". Infatti, un computer memorizza dati in forma binaria: 0 o 1 (il famoso bit). Abbiamo, dunque, un sistema a due stati. In "teoria dell'informazione" l'entropia è data dal logaritmo del numero di stati accessibile al sistema (e ciò è valido anche in Meccanica statistica). Abbiamo, dunque, che l'entropia di tale sistema è ln(2), che è un valore estremamente piccolo. Tuttavia, i circuiti elettrici/elettronici dissipano energia per effetto Joule. Attraverso un sistema di raffreddamento (ventole), il calore viene trasferito nell'ambiente, per cui aumenta l'entropia di quest'ultimo. In tal modo siamo a cavallo, perché il sistema computer+ambiente è isolato, e quindi la sua entropia non può fare altro che aumentare. Infatti, a una riduzione dell'entropia del computer (che crea un ordinamento nei suoi stati) corrisponde a un incremento di entropia nell'ambiente. Quest'ultimo è ovviamente generalizzabile all'intero universo (che è un sistema isolato e chiuso).
(altro…)

Posted in Fantasticherie cognitive | No Comments »

[¯|¯] Il libero arbitrio: una questione termodinamica?

sabato, Novembre 29th, 2014

Dalla condivisione dello stato di Facebook di uno dei miei contatti:

mi sono venute alcune idee sulla questione del cosiddetto libero arbitrio. Una precisazione: le suddette idee vanno prese con le molle, perchè si tratta di speculazioni (deliri? 🙂 ) e nulla di più.
Ciò premesso, denotiamo con X un qualunque sistema cognitivo (umano, calcolatore). In poche parole, X è un sistema "in grado di pensare" e, soprattutto di ricordare (in effetti, il nocciolo della questione è legato alla memoria). Osserviamo subito che se X è un calcolatore, la sua memoria è praticamente infallibile. Ciò è dovuto al valore estremamente basso dell'entropia dei suoi stati logici. Infatti, la memoria di un calcolatore è un sistema a due stati, e utilizzando la nota formula (dalla meccanica statistica), si ottiene per l'entropia (k_B è la costante di Boltzmann):

entropia,termodinamica,meccanica statistica

Se, invece, X non è un calcolatore:

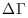dove è il volume dello spazio delle fasi associato al sistema, i.e. il numero di stati di singola particella. È chiaro che qui 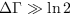, onde una qualunque interfaccia umana avrà un'entropia del proprio sistema cognitivo, maggiore dell'entropia della memoria di un calcolatore. In altre parole, un calcolatore ha una "memoria infallibile" proprio perchè è un sistema "più ordinato".
(altro…)