Coronavirus. Cercasi disperatamente curva logistica
sabato, Marzo 14th, 2020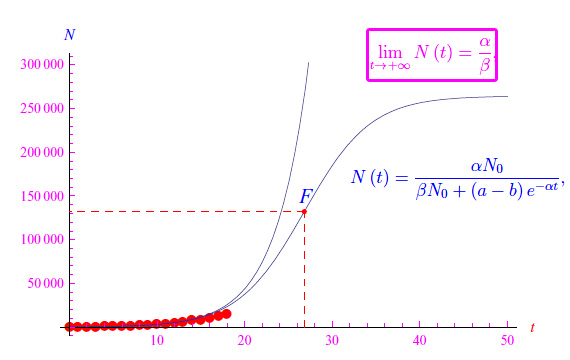
Esaminiamo l'approccio standard per la ricerca di una logistica per il sistema dinamico in esame. Come è noto, si assegna un'equazione differenziale del tipo Riccati che nel nostro caso si scrive:
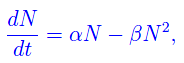
dove α è il valor medio dei vari parametri calcolati in precedenza, mentre ß > 0 è un parametro ignoto che agisce da fattore di smorzamento dell'esponenziale. Integrando tale equazione differenziale con la condizione iniziale N(0)=N0=221, dopo qualche passaggio si ottiene:
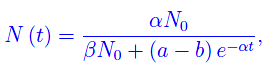
da cui emerge il comportamento asintotico:
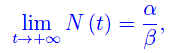
e il comportamento esponenziale a tempi brevi. Con i dati in nostro possesso presi dal sito web della Protezione civile, abbiamo visto che un valore affidabile del parametro ß è
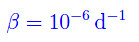
Infatti, plottando la soluzione otteniamo l'andamento riportato in fig. 1. Inoltre, studiando la derivata seconda si stabilisce l'esistenza di un punto di flesso a tangente obliqua, visibile nella predetta figura. L'ascissa è
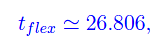
corrispondente al 31 marzo.





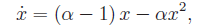
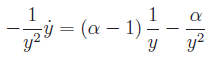



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











