[¯|¯] Derivazione assoluta e relativa di una funzione vettoriale. Lemma di Coriolis

giovedì, Gennaio 9th, 2020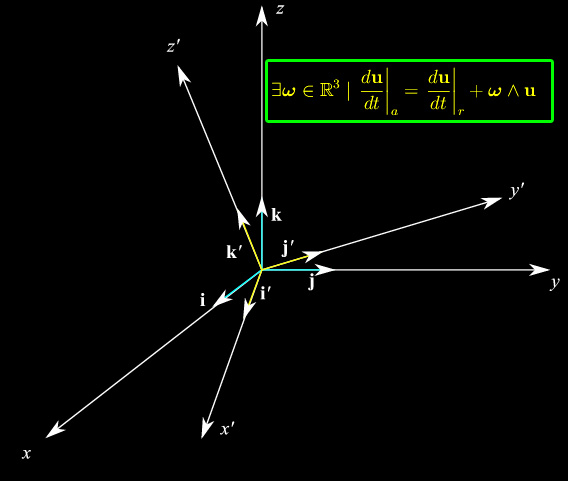

derivazione assoluta e relativa di una funzione vettoriale,lemma di Coriolis
Fig. 1

Sia K'(O'x'y'z') un sistema di riferimento rotante rispetto a un sistema di riferimento K(Oxyz) che possiamo ritenere fisso. Inoltre, è O'=O come in fig. 1. Scriviamo la rappresentazione cartesiana di una funzione vettoriale u(t) nel sistema di riferimento K:


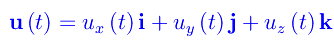
La stessa funzione ha in K', la seguente rappresentazione cartesiana:

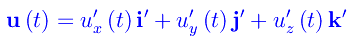
In altri termini, denotiamo con ux(t),uy(t),uz(t) le componenti del vettore u rispetto alla base ortonormale {i,j,k}, e con u'x(t),u'y(t),u'z(t) le componenti dello stesso vettore nella base ortonormale {i',j',k'}.
(altro…)



Posted in Fisica generale 1, Meccanica analitica, meccanica razionale | No Comments »