Definizione di limite: funzione che tende all'infinito

venerdì, Febbraio 12th, 2021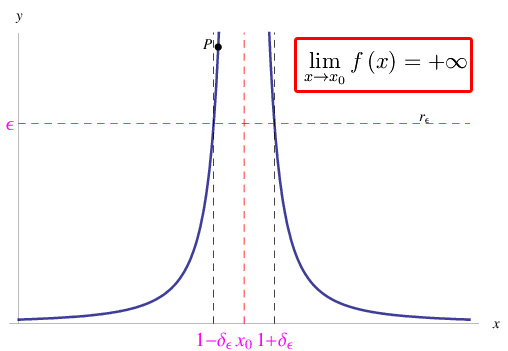

Nella lezione odierna diamo la definizione di divergenza di una funzione per x che tende a un punto di accumulazione (al finito) x0. Locuzioni alternative sono: 1) la funzione tende a "+ infinito" (+oo) [o a "- infinito" (-oo)] per x che tende a x0; ) la funzione ha per limite "+ infinito" (+oo) o "- infinito" (-oo) per x tendendte a x0.
Tali locuzioni sono compattate nel simbolo riportato in fig. 1.
Nel caso di divergenza positiva, significa che in un intorno di x0 la funzione è definitivamente maggiore di un numero reale positivo assegnato arbitrariamente (comportamento simile per la divergenza negativa, ove la funzione è definitivamente minore di un qualunque numero reale negativo).
Le predette definizioni hanno una notevole interpretazione geometrica che conduce fisiologicamente alla nozione di asintoto verticale del diagramma cartesiano (o grafico) di una funzione reale di una variabile reale.
Viene infine sottolineata la seguente circostanza: una funzione può benissimo essere definita in un punto x0 ove ha per limite infinito. Ciò non deve sorprendere in quanto il valore assunto da f non ha relazione alcuna con il limite corrispondente.

Scarica la lezione in pdf
(altro…)

Posted in Analisi Matematica I | No Comments »

Esiste questo limite?

mercoledì, Gennaio 13th, 2021

limite funzione più variabili, definizione di limite — **Fig. 1**

Risolviamo alcuni degli esercizi proposti da Calculus and Analytic Geometry
Esercizio

Sapendo che |sin(1/x)| < = 1, cosa potete dire riguardo al seguente limite

Soluzione
Poniamo

Questa funzione è definita in

cioè su tutto il piano cartesiano xy escluso l'asse y. Ovviamente l'origine delle coordinate (0,0) non appartiene all'insieme di definizione, ma è comunque punto di accumulazione per tale insieme. Congetturiamo (in analogia al caso unidimensionale)