Il problema delle condizioni iniziali nel Pendolo semplice

venerdì, Giugno 12th, 2020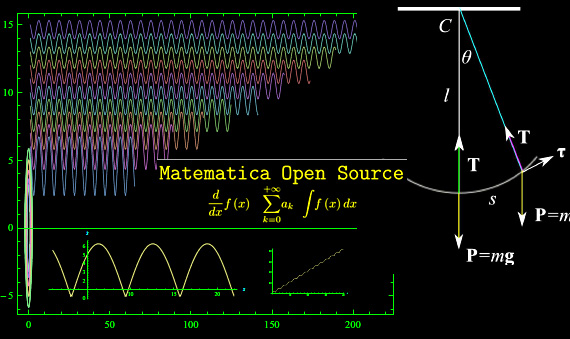

pendolo semplice,equazioni differenziali,condizioni iniziali

Naturalmente, possiamo integrare l'equazione differenziale del moto del pendolo semplice con una condizione iniziale che prevede una velocità iniziale non nulla. Ad esempio

che nel sistema di ascisse curvilinee assegnato, ci dice che il pendolo non è inizialmente lasciato libero, ma "spinto" verso l'alto (lungo la traiettoria). Superato un certo valore, il pendolo sembra allontanarsi definitivamente dal punto iniziale, come può essere visto integrando numericamente l'equazione differenziale. Più precisamente, assegnato un pendolo di lunghezza unitaria (l=1m), con condizioni iniziali:

otteniamo il diagramma orario riportato in figura:

nvestighiamo su questo comportamento, plottando la velocità scalare in funzione del tempo nel grafico di figura:

da cui vediamo che è sempre positiva. Ciò implica l'assenza di istanti di arresto con inversione del moto. In realtà, l'equazione differenziale del moto non tiene conto dell'effettiva configurazione del vincolo (il punto materiale non può percorrere l'intera circonferenza), per cui superato un certo valore della velocità iniziale, il punto riesce a percorrere l'intera circonferenza un numero infinito di volte (per t→+∞).

È interessante studiare il comportamento del sistema nel cosiddetto piano delle fasi, ovvero un piano cartesiano dove in ascisse riportiamo la grandezza s e in ordinate la derivata prima, i.e. la velocità scalare. Otteniamo il grafico (traiettoria di fase) riportato in fig.

Infine, facendo variare parametricamente la velocità scalare iniziale, otteniamo la famiglia di traiettorie di fase riportate in fig.

Indice delle lezioni/esercizi

Posted in Fisica generale 1, meccanica razionale | No Comments »

[¯|¯] Un problema di Cauchy la cui soluzione non può essere messa in forma esplicita

domenica, Agosto 13th, 2017

equazioni differenziali,problema di cauchy,condizioni iniziali — **Fig. 1. Alcune curve integrali dell'equazione differenziale assegnata**

Risolvere il problema di Cauchy

Soluzione
L'equazione si integra per separazione di variabili
equazioni differenziali,problema di cauchy,condizioni iniziali

che definisce implicitamente l'integrale generale. Imponiamo la condizione iniziale y(3)=-1:
equazioni differenziali,problema di cauchy,condizioni iniziali

Ne concludiamo che l'integrale particolare che risolve il problema di Cauchy assegnato è implicitamente definito dall'equazione
equazioni differenziali,problema di cauchy,condizioni iniziali