[¯|¯] Omeomorfismi, spazi di Hausdorff. Varietà topologica
sabato, Aprile 1st, 2017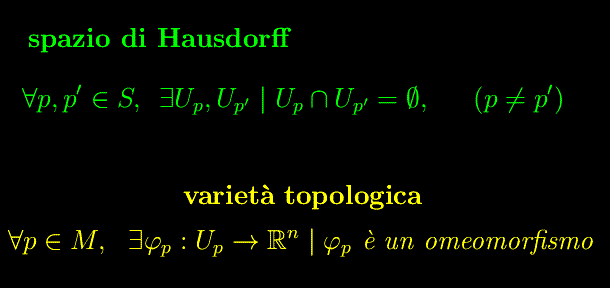
Premessa. Omeomorfismi
In precedenza abbiamo lavorato sullo spazio Rn, dotandolo di una struttura di spazio vettoriale topologico. In questo post vogliamo generalizzare tale nozione, nel senso che ci riferiremo a un generico spazio topologico e non necessariamente a Rn, per cui è necessario rammentare le nozioni basilari di topologia, prima tra tutte il concetto di omeomorfismo, che nel caso particolare di Rn, si definisce nel seguente modo:
Definizione
Se A è un sottoinsieme di Rn un'applicazione
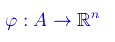
è un omeomorfismo se φ è continua in A ed è ivi dotata di inversa continua in φ(A) (contenuta ovviamente in Rn. In tal caso si dice che i sottoinsiemi di Rn
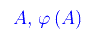
sono omeomorfi.
Esempio
Nello spazio vettoriale topologico R¹ consideriamo l'applicazione
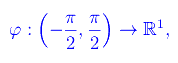
così definita:
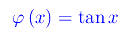
φ(x) è continua in (-π/2,π/2) ed è ivi dotata di inversa continua in R¹:

Ne concludiamo che tanx è un omeomorfismo da (-π/2,π/2) a R¹, onde l'aperto (-π/2,π/2) è omeomorfo a R¹ attraverso tanx.
Spazi di Hausdorff. Varietà topologica
Dando per scontata la nozione di intorno di un punto p appartenente a uno spazio topologico(S,Θ), definiamo:
Definizione
Uno spazio di Hausdorff è uno spazio topologico (S,Θ) tale che
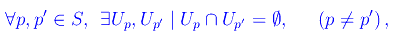
dove Up,Up' sono intorni di p e p' rispettivamente.
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











