[¯|¯] Introduzione al concetto di Varietà differenziabile

Marzo 31st, 2017 | by Marcello Colozzo |

varietà differenziabile,spazio topologico,spazio metrico — **Fig. 1**

Le ambiguità riscontrate nella definizione di curva regolare, si risolvono in "un colpo solo" attraverso la nozione di varietà differenziabile. Per introdurre tale importante ente geometrico sono necessarie alcune premesse.

Lo spazio euclideo a n dimensioni

In questa esposizione seguiremo il testo Introduzione ai metodi della geometria differenziale dove viene utilizzata la convenzione degli "indici in alto" per denotare gli elementi delle n-ple ordinate che compongono l'insieme Rⁿ:

con l'ulteriore convenzione di indicare con x (non grassettato) il generico elemento del predetto insieme. Cioè
varietà differenziabile,spazio topologico,spazio metrico

Ciò premesso, definendo la funzione distanza:
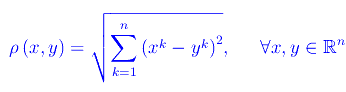
varietà differenziabile,spazio topologico,spazio metrico

L'insieme Rⁿ assume la struttura di spazio metrico. Chiamiamo tale spazio spazio euclideo a n dimensioni. Inoltre, la metrica induce in Rⁿ una struttura di spazio topologico. In tale topologia gli aperti sono gli insiemi di punti:
varietà differenziabile,spazio topologico,spazio metrico

per un assegnato ξ=(ξ¹,...,ξⁿ) di Rⁿ e R>0 scelto ad arbitrio.

Se nel predetto spazio topologico introduciamo le leggi di composizione:

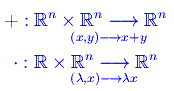
vediamo facilmente che esse verificano gli assiomi di spazio vettoriale, per cui abbiamo in definitiva uno spazio vettoriale topologico.
Le nozioni appena esposte possono essere riassunte nel seguente schema:
varietà differenziabile,spazio topologico,spazio metrico

***
Sia A un aperto dello spazio vettoriale topologico Rⁿ.
Definizione
Una funzione:

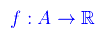
si dice analitica in x₀ (puntto di A) se è sviluppabile in serie in ogni intorno di x₀. Se f è analitica in ogni x di A, diremo che è analitica in A.

Definizione

Una funzione f analitica nell'aperto A si dice di classe ω su A e si scrive

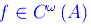
L'appartenenza alla classe C^ω implica l'appartenenza alla classe C^oo, dove
varietà differenziabile,spazio topologico,spazio metrico

essendo C^k l'insieme delle funzioni continue in A ed ivi dotate di derivate parziali continue di ordine <=k. Per quanto precede: varietà differenziabile,spazio topologico,spazio metrico

Ma non viceversa:

Ad esempio, nello spazio vettoriale topologico R¹:
varietà differenziabile,spazio topologico,spazio metrico

così definita
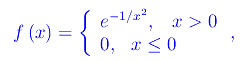
varietà differenziabile,spazio topologico,spazio metrico

che è continua a sinistra in x=0. Per il comportamento a destra rileviamo
varietà differenziabile,spazio topologico,spazio metrico

Per cui la funzione è continua in x=0 e, quindi, in R. La derivata prima è:
varietà differenziabile,spazio topologico,spazio metrico

Calcoliamo

Eseguendo il cambio di variabile t=x^-1:
varietà differenziabile,spazio topologico,spazio metrico

onde

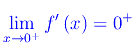
Cioè f'(x) è continua in x=0 e, quindi, in R. Analoga conclusione per f^(k)(x) per ogni k intero naturale. Ne consegue
varietà differenziabile,spazio topologico,spazio metrico

Tuttavia se sviluppiamo in serie in un intorno di x=0:
varietà differenziabile,spazio topologico,spazio metrico

D'altra parte
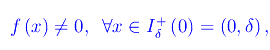
varietà differenziabile,spazio topologico,spazio metrico

Quindi

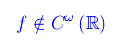
Definizione
Nello spazio vettoriale topologico Rⁿ sono definite n applicazioni:

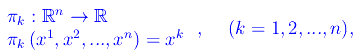
che si dicono proiezioni coordinate.

Sia data l'applicazione
varietà differenziabile,spazio topologico,spazio metrico

essendo A un aperto di Rⁿ. Riesce:
varietà differenziabile,spazio topologico,spazio metrico

La derivata rispetto alla variabile x^j è
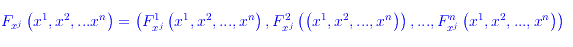
varietà differenziabile,spazio topologico,spazio metrico

A tale applicazione possiamo associare n funzioni
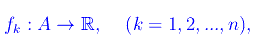
varietà differenziabile,spazio topologico,spazio metrico

mediante la composizione:
varietà differenziabile,spazio topologico,spazio metrico

avendosi

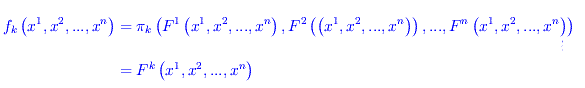
Risulta manifestamente
varietà differenziabile,spazio topologico,spazio metrico

Ad esempio, nello spazio vettoriale topologico R², sia data l'applicazione:
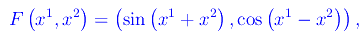
varietà differenziabile,spazio topologico,spazio metrico

per cui F è di classe C^oo su R². Riesce
varietà differenziabile,spazio topologico,spazio metrico

con f_k di classe C^oo su R². In fig. 1 riportiamo il grafico delle funzioni f_k(x¹,x²).

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.