[¯|¯] Limiti di funzioni: quando la regola di De L'Hospital non è applicabile
mercoledì, Maggio 30th, 2018
Sul gruppo facebook di matematica relativo a questo blog, un utente ha proposto il calcolo del seguente limite:

manifestamente equivalente a
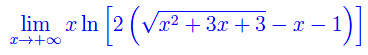
Dopo aver mostrato che l'argomento del logaritmo converge a 1, si ha che tale limite si presenta nella forma indeterminata 0·oo. Riconducendo tale forma alla 0/0 e applicando la regola di De L'Hospital, il limite non viene calcolato in quanto si ripresenta la 0·oo. Un altro utente ha risolto applicando l'analisi matematica non standard. Dal momento che non conosco tale paradigma di calcolo, cercherò di applicare una qualche manipolazione in modo da rimuovere l'indeterminazione.
In realtà tale limite appartiene a una classe di limiti derivanti da

dove:
-
f1(x) diverge positivamente per x->x0:
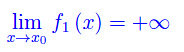
- f2(x) converge a 1 per x->x0:
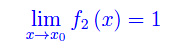


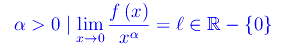
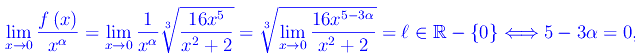


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











