[¯|¯] Grafico di una relazione

Dicembre 2nd, 2014 | by extrabyte |

Sia 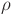una relazione in un insieme A:

relazione in A

Definizione
Dicesi grafico della relazione 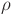sottoinsieme di A2:

grafico di una relazione

Cioè, l'insieme delle coppie ordinate di elementi di A in relazione tra loro.



Premettiamo alcune definizioni relative al prodotto cartesiano.

Definizione
Dicesi diagonale di l'insieme:

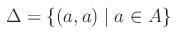
diagonale prodotto cartesiano

Comunque prendiamo a,b in A le coppie ordinate (a,b), (b,a) si dicono simmetriche rispetto alla diagonale.

Esempio
Se 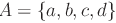, risulta:

diagonale, prodotto combinatorio, insiemi

Definizione
Assegnato 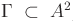, si chiama simmetrico di 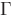e si indica con , l'insieme i cui elementi sono i simmetrici degli elementi di gamma00x1.gif rispetto alla diagonale.


Definizione

Da tale definizione segue immediatamente che comunque prendiamo una relazione 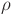in A, risulta:

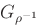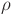dove è il grafico della relazione inversa . Le proprietà di diventano rproprietà di 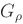e 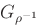. Infatti, sussiste la seguente proposizione:
Proposizione



No TweetBacks yet. (Be the first to Tweet this post)

Tags: , ,

Articoli correlati

Commenta l'esercizio