Verifica di un limite
Febbraio 5th, 2021 | by Marcello Colozzo |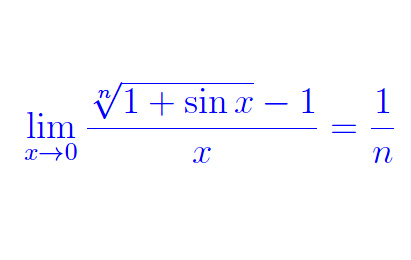
Si chiede di calcolare un limite senza applicare la regola di De L'Hospital (in quale forma indeterminata si presenta il rapporto?). Qui n è un intero naturale non nullo. È possibile generalizzare considerando un esponente reale?
We are asked to calculate a limit without applying De L'Hospital's rule (in which indeterminate form does the relationship appear?). Here n is a non-zero natural integer. Is it possible to generalize by considering a real exponent?
No TweetBacks yet. (Be the first to Tweet this post)
Tags: analisi matematica 1, Forme indeterminate, limiti di funzioni
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











